Page 2 of 3 •  1, 2, 3
1, 2, 3 
 1, 2, 3
1, 2, 3 
 The lord of hungerLevel Two
The lord of hungerLevel Two
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
February 28th 2020, 12:50 am
Isv ragdolling
 Latham2000Level Three
Latham2000Level Three
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
February 28th 2020, 7:53 am
ISV's post is impressive. T4V.
 Nute_ChethrayModerator
Nute_ChethrayModerator
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
February 28th 2020, 5:48 pm
Looks neat, will check out tomorrow
 BreakofDawnLevel Seven
BreakofDawnLevel Seven
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
February 28th 2020, 7:18 pm
 IGLevel Four
IGLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 8:41 am
Section I - Vader’s Immense Growth (or Lack Thereof)
No, my argument does not hinge on the idea that Vader’s growth was predicated around that single boost. The boost is not representative of his average annual growth. If somebody gains a massive power boost, we can’t apply that to their normal growth. We see Jacen Solo in Legacy of the Force: Sacrifice gains a massive sacrificial power boost from killing Mara Jade. He doesn’t gain these massive power boosts every day, not every week, nor every month. Likewise Anakin gains a massive power boost by jumping to the DS. Yet he isn’t going to be gaining boosts akin to that every other day or so, had he survived.
Likewise, Vader’s killing of Roan Shryne “firm[ed]” Vader’s faith in “the power of the dark side”. You haven’t provided evidence for why Vader going from, as you’ve said “a walking pile of burn garbage” to one whose “true apprenticeship could begin” is representative of normal growth. It’s evidently indicative of a massive boost in power. As for my point about Vader’s growth, it doesn’t require a citation, as I’m appealing to common sense. We see masters as they grow closer and closer to achieving their potential stagnating. Yoda says that he used to be able to lift 5 Muntuur stones, now (around pre-TPM iirc) he’s only able to lift 4. Vader hasn’t achieved nearly as much of his (revamped) suited potential in 19 BBY as he has in 10 BBY, so logically he’ll grow more when he has more of his potential to achieve than less, evident by my Padawan analogy.
Except I wasn’t comparing Anakin to Obi-Wan at all. I literally pointed out two periods of their lives and compared the growth there to another period in their lives. I compared Anakin’s TPM-AOTC Growth to his AOTC-ROTS growth and stated that he grew more during the latter period than the former. I likewise compared Kenobi’s growth in the two time periods. Given that both of the characters’ growth is not linear, it’s logical to proclaim that all growth isn’t linear. Other examples of growths that aren’t linear is Sidious’ from TPM to ROTS compared to ROTJ to DE, therefore showing that there’s no validity in claiming linear growth.
My statements of incredulity were in regards to the fact that Vader’s growth being linear is completely unfounded and that Luke’s 19 ragdoll gap superiority to Shryne, to be quite frank, is utter bull. Tell me ISV, if Vader grows a ragdoll gap a year, why does he struggle with Ben Kenobi? Consider that under your premise of Vader >> ESB Luke > Ben ~ ROTS Kenobi ~ Dooku that you fail to account for AOTC Anakin. Anakin is a greater prodigy with 10 years of formal training, as a sharp contrast to Luke being a lesser prodigy with only 7 months (as you’ve cited later on in your post) of informal training. Logically then, given Anakin has a greater potential than Luke, he is more powerful than Luke. Dooku dismisses Anakin during one of his “flashes of brilliance”, times when Anakin performs at a far, far better state than his normal one. Thus making it evident of Dooku’s (vast) superiority to ESB Luke. Lucas also indicates that Luke’s training is subpar comparative to a normal Jedi in the following quote:
None of them actually make it clear that Ben gave up. I’ve always been of the opinion that he’s thrown the fight, something that the DK book quote makes evident. As for your point on Chee, the tweet is in response to a question about the 6, 4, 2 quote. Meaning that this is supporting evidence that the 6, 4, 2 argument stands. Chee follows Lucas’ lead on this, and declares that Obi Wan is indeed stronger than Vader, but power levels (raw power a force wielder can use) aren’t the only factor in a fight.
As for your arguments on the quote’s validity, the first two revolve around the core idea that the terminology “maybe” and “probably” are ambiguous, and that it makes no sense to declare that Ben > Vader solely on these quotes. Yet the general idea is that Chee’s quote allows reconciliation of the idea Ben > Vader. We see how his tweet was in response to a question about the quote, where he goes along with Lucas’ intent and declares Ben > Vader in raw power is canonically fact.
Which is all fair, but being a better combatant than somebody isn’t being more powerful than them. Ben’s an old man, so while his raw power is still at the level of Vader, his combatative skill is, to be quite frank, shit. To contrast, Luke lacks the raw power that Obi-Wan has, but he’s young, so naturally he’s more mobile than a man nearing the age of 60.
Here however, you try to claim that Luke’s mobility and greater speed are evidence of why he’s faster and more powerful than Ben. The double standards here astound me. You yourself claim that Luke’s greater speed than Ben shows superiority, but when I cite Dooku moving so fast that Kenobi is incapable of throwing up a defense to block his attacks, you claim that it’s an incorrect comparison? Here, I actually have to point out a glaring flaw with your entire logic, namely Vader’s linear ragdoll gap growth. According to you, Vader grows a ragdoll gap each year, meaning he’s jumped 3 from ANH to ESB, and Luke being outside his ragdoll range means that he’s at least a single ragdoll gap above Ben Kenobi, whom you claim is ~ ROTS Kenobi and therefore ~ Dooku. Yet not even Darth Sidious or Yoda are capable of ragdolling Dooku or Obi-Wan. In fact, Yoda is incapable of doing this to the degree that he’s forced to fight Dooku and push him back “slowly”. Somehow Vader as of ROTJ is a ragdoll gap above the likes of Yoda and Darth Sidious? That’s a completely insane argument, even by your standards. For one, Lucas himself explicitly states Vader in his suit could never become as powerful as Sidious was. He explicitly claims Vader can only become “80%” of Sidious. And that’s Vader’s suited potential, not his actualized power as of Return of the Jedi.
I was referring to ROTS Yoda. Whether Vader can or cannot defeat Yoda as of ANH (which I highly doubt, and it’s completely irrelevant anyway) is something I doubt we need to debate here. If Luke > all Jedi before that Vader’s met, that’s evidently including Windu, ROTS Kenobi, Yoda, etc, and the claim that ESB Luke > Yoda is something that’s easily refutable, namely through Lucas’ comments on it.
The quote clearly referring to Vader in his suited iteration means Luke is a greater combatant than Ben, but nothing in regards to their raw power with the force.
Meaning that Kenobi’s old age makes him a far slower duelist. One’s overall skill is a mix of raw power and technical skill, raw power affecting your augmentation and overall combat performance. Kenobi is explicitly “not the duelist he once was”, indicating a great disparity between his ROTS and ANH iterations. His ability in the force has diminished, as has his technical skill, leaving him a far worse combatant than usual.
Section II - Dooku Ragdolls
Obi-Wan is surprised that Dooku can hit him, yes, but that’s not refuting my argument. If Dooku is capable of taking the master of a completely defensive style off guard and then taking him out, then why can he not do the same to Vader? Vader’s style “lacks the polish of lifelong masters”. He lacks the technical refinement that all “lifelong masters”, such as Kenobi, Windu, Dooku, Yoda, etc have. Again the double standards. Why is speed not denoting anything? Your entire argument for Ben < ESB Luke revolves around the central premise that he’s faster and more mobile than him, so he has more strength in the force through a speed comparison. Given that this is an active combat situation, perhaps Kenobi is off-guard, yes, but that doesn’t change the fact that before he can so much as react, we see Dooku move so quickly that Kenobi cannot counter his attack. If you can make speed comparisons, you have to deal with them too. This is no “burst of speed in equals”, as you claim. Dooku’s capable of fighting at this level against two high level foes, Anakin and Obi-Wan at the same time. Consider that if there’s a duo and both of them stand a chance at soloing, then there’s going to be an immense stomp happening. That clearly doesn’t happen here. You cite Kenobi “stonewalling” Dooku earlier in your first post, yet Dooku’s caught utterly by surprise at Kenobi’s rapid change in form. Just months from ROTS, Windu fights Dooku, and Windu attempts to strike Dooku down. Dooku seems to easily deflect the blow and mocks Windu to his face about it. Likewise Dooku is able to take blows from Yoda himself on Vjun, and is only pushed back “slowly”, while taunting Yoda the entire time. In AOTC Dooku and Yoda fight in a relatively close fight, with an exhausted Dooku managing to exhaust Yoda (I’ll cite that in my rebuttal). We then see that Dooku is capable of contending and practically beating Yoda in 20 BBY in the comic Yoda Uncovered.

We clearly see here that he contends with Yoda in bladelock, then Yoda jumps away and attempts to flip over Dooku, but Dooku blasts him away with lightning. This is an undeniable showing of nigh-parity. If Dooku, as you claim, is extremely far beneath Yoda per the tiering system, then why is he able to perform this well? Is it because perhaps Dooku is not so weak that he would be stomped by his master of by Yoda? As you claim, maybe Dooku doesn’t have raw power on par with the PT titans, or even near them (I’m not claiming this is true, to clarify). But even if this is true, Dooku’s ability to contend with foes with (as you claim) far greater raw power than him is an undeniable advantage he has. Vader just hasn’t shown the ability to compete with a tier 9 fighter like Yoda the way Dooku has. Dooku has been able to resist Yoda’s offensive onslaught and leave his former master exhausted for it all those times. To contrast, Vader has low showings against fodder like a post-prime An’ya Kuro



[....]


Should we consider Darth Vader, a character that has unfavorable showings against fodder like Kuro to be a top tier? Should we consider Vader, somebody that’s shown time and time again his utter incompetence when dealing with powerful foes to be on par with a master such as Dooku? Should the character holistically portrayed to be with the likes of TPM Maul, or even TPM Kenobi be considered for superiority to somebody that gave Yoda the fight of his life several times and practically beat him once?
The attack had been too sudden, yes. But this is active combat, there is a time Kenobi can be taken by surprise, but the fact that Dooku’s able to do so means that he’s able to engineer and exploit openings in others’ defenses, something that Vader will inevitably fall to. We see in Vader’s duels with Luke during ESB and ROTJ that he is prone to utilizing long, sweeping strikes. Dooku can easily take advantage of this, the example being his fight with Kenobi in ROTS, where he’s able to easily take Kenobi out by exploiting the openings he leaves. Vader’s somebody that has been countered by a lesser prodigy than Anakin in Luke during ESB, even being injured in it.
Expanding on Dooku’s superiority to Kenobi:
https://www.youtube.com/watch?v=OcXaicGvcvA
In the link above, Dooku fights both Kenobi and Skywalker evenly (if not holding an advantage) for a period of over a minute. At approximately 1:01, we see Dooku remove Kenobi from the fight with ease for a time. Throughout we also see Dooku’s ability to fight with great mobility, something that gives him an undeniable advantage against Vader’s restricted mobility. At around 2:04, we see Dooku utilize a force blast that knocks back both Anakin and Obi-Wan, pushing them to their knees. Given the disproportionate strength of a barrier and the fact that both Kenobi and Skywalker had them up at the time, we can conclude that Dooku’s superiority to Kenobi is all but fact. Then we see Dooku overpowering Kenobi’s superior in Anakin in bladelock at 2:52.
As for Revenge of the Sith itself, we see numerous times in the fight Dooku’s evident superiority to Kenobi:
Dooku is able to casually throw chairs at Anakin while the latter charges at Dooku, simultaneously holding Kenobi at bay one-handedly. Consider that Dooku shows seemingly no strain throughout, and is able to counter Kenobi while utilizing the force to throw stuff at Anakin.
Dooku’s able to “effortlessly” counter Obi-Wan’s attacks, another showing of superiority.
You claim that the “whipcrack” of energy ragdoll and the ragdoll shown in the movie where Dooku kicks Anakin back and then chokes Kenobi are the same. Yet this is evidently not the case. The scene in question, where Kenobi attempts to double-team Dooku and gets caught off-guard is depicted after Dooku flings Kenobi across the room effortlessly.
This part specifically is where Kenobi is removed from the fight, similar to the section of the JN you cited. The part that Dooku flings Kenobi away with a “whipcrack” of power is earlier on, and is depicted in the film as Dooku pushing Obi-Wan, not choking him. There’s no evidence that Kenobi is caught by surprise when flung across the room by surprise the first time, and while it’s certainly possible that he only had a passive barrier up, Dooku still effortlessly chucks him away, and since there’s no evidence to the contrary, I can attribute this to Dooku’s own skill and power being greater than that of Kenobi’s.
Here’s the clip showing specifically what I was referencing:
https://www.youtube.com/watch?v=eYT3ctPuVRw (1:28).
The quote from the ROTS JN you provided states that Kenobi was caught off guard when Dooku choked him, but that’s clearly not what Stover references during the “ragdoll” sequence of his novel.
Except there’s no evidence that Kenobi was caught by surprise and there’s no evidence that this was merely a quick burst of speed as opposed to Dooku having just that much better augmentative capability than Kenobi does. You mention how barriers are easy to throw up in your Krayt comparison, but Cade isn’t using TK on Krayt then, he completely catches Krayt by surprise and takes him out with a saber attack. To contrast, Dooku augments himself sufficiently that Kenobi isn’t given the option to react in the example I’ve cited.
1. Dooku’s ability to counter attacks from Mace Windu a few months before ROTS with ease and nearly stalemate Yoda on several occasions, combined with the fact that Dooku is caught off-guard by Kenobi and Anakin’s change in form from Shii-Cho/Ataru to Soresu and Shien to Djem So respectively shows your argument is wrong.
2. While Kenobi may not have had an active barrier up, he certainly had a passive barrier up given the situation is in active combat, and as we’re speaking of two separate incidents within the fight, it’s safe to say that Kenobi wasn’t necessarily caught off-guard/by surprise.
3. Yet Kenobi wasn’t caught off-guard by Dooku’s assault, there’s no evidence saying he was. Dooku is able to augment himself so much that Kenobi is unable to defend himself and is flung across the room.
Kenobi being able to deflect force blasts is not a showing of parity whatsoever. Kenobi’s barrier allows him to do so. In the Gillardian tiering system you cite, Kenobi is explicitly an “8”. It’s completely false to claim that Kenobi magically jumps to a 9 on Mustafar. Gillard uses “Obi Wan is an 8” as a blanket statement encompassing ROTS. Consider that Kenobi and Anakin both have intimate knowledge of each other’s forms, and while this link goes both ways, Kenobi benefits moreso from it than Anakin, as Anakin’s gone essentially batshit in this fight, and Kenobi being a defensive fighter gains more of an advantage the whole fight if he knows what his opponent’s next move will be. Considering that Kenobi also gives ground the whole fight, it’s pretty obvious that Anakin holds an upper hand… until he makes a fatal blunder.
And the quote referencing their duelling abilities was my point. Considering that dueling abilities are related to 2 things, augmentation and technical skill. Augmentation is directly related to one’s raw power in the force, and therefore since Kenobi’s skill as a duelist has regressed, his force power has likewise. Since you’ve not responded to my claim that Vader’s comment that “your powers are weak, old man”, means that Kenobi’s powers have regressed since ROTS, I’ll take that as a concession.
Except Luke makes an earnest attempt at lifting the X-Wing and fails utterly. His confidence or lack thereof in his abilities doesn’t change the fact that this kind of TK is something he deems beyond himself with good cause--he simply cannot do so.
Characters grow only through conflict, per Kreia. Considering that Dooku is involved in a massive galactic scale war, it’s pretty obvious that he grows a lot. Consider also that Dooku throws the ships and cruiser “with ease”. My comparison was simple, that Dooku’s TK is far, far beyond ESB Luke’s. Dooku being able to casually throw around cruisers (while amped, yes) and then undergoing 3 years of immense growth is a testament to his power. You haven’t sufficiently demonstrated that the nexus of Korriban circa 22 BBY is strong enough that it means Dooku cannot throw cruisers around when not amped by it. Perhaps when not amped by Korriban Dooku won’t be throwing ships around with such casual ease. My point remains however, that Dooku’s TK is demonstrably far beyond what Luke as of ESB has shown.
To put (someone or something) to the test is defined as “to cause (someone or something) to be in a situation that shows how strong, good, etc., that person or thing really is”. Meaning that Yoda is the only one thus far that has shown how strong Dooku really is. That doesn’t mean Anakin couldn’t have pressed him though. Toying with one explicitly means that you’re playing around with them to amuse yourself. Dooku is pressed by Anakin to a degree, but it isn’t something that makes Dooku utilize his full ability.

And I see no reason for said feats of strength to be referring to raw power in the force. Like, we clearly see Anakin being far superior to Vader in terms of the force, and there’s no reason that Vader’s cybernetic enhancements should make up that gap. Your argument that Vader jumps a ragdoll gap a year clearly falls flat when we take into account the fact that if in 19 BBY, Vader with aug + cybernetics > Anakin with Aug, then by 4 BBY, he should be tossing around the PT Titans with ease.
For your point about Mace fighting Dooku: it’s fairly evident from how short the fight is (literally one or two exchanges) that Mace can’t get a feel for Dooku’s strength from it. Considering Dooku’s fought on par with the likes of Yoda and not yielded in bladelock, your claim that Vader can physically overpower Dooku when Vader’s already shown himself to be much weaker than Yoda is incorrect. Considering that I've given and backed up evidence for why Vader <= AOTC Anakin, I think it's safe to say that no, Vader isn't striking with "more deadly invincibility" in that comic.
Section III - Parity to Yoda, Reaffirmed
Well yes, but it’s showing that he’s at least ~ Yoda, something that other sources show as well.
Have you read Bloodlines? Caedus flow-walked into the past. He basically time-travelled, to be concise. He isn’t going off of old records and what Luke could tell him, evident from Caedus witnessing a scene that there is likely no record of--Anakin being denied mastery.
Except this isn’t referring to Anakin’s potential whatsoever. Sidious didn’t say “Anakin has the potential to be stronger than myself”. Sidious says that as of that minute, Anakin is possibly stronger than himself.
Where does Gillard ever claim Anakin starts ROTS as an 8?
Yoda is actively drawing upon the dark side throughout this fight. It’s pretty evident in the book itself. “In the dark, drunken Vjun air, Yoda was terrible to behold”. “And yet, even here on Vjun, where the dark
side whispers and whispers to me...love you enough to destroy you I do”.
Yoda utilizing the dark side doesn’t mean that he’d be hindered or conflicted. There’s nothing that actually hints at conflict. Yoda states he’s going to kill Dooku, and that the DS “whispers and whispers” to him. Given that you’re using the author quote over there, I think that means that you really won’t object to my use of it as well. And Stewart explicitly states, “so my instinct would be that he’s tapped into Vjun”, and that “Yoda and Dooku are both like surfers in a place with big waves. The more expert the surfer, the more they can do with that power”. Meaning that Yoda is utilizing the nexus of Vjun to a greater effect than Dooku is, but he’s only pushing him back, “slowly, slowly”.
Except Revenge of the Sith wasn’t released yet. Until something is published (released in this scenario), it has no canonical validity. There’s a reason that Supernatural Encounters isn’t canon, it isn’t published. Meaning that by default, Hidalgo is referring to AOTC Anakin because Revenge of the Sith just doesn’t exist yet as a canonical entity.
Well skill is directly related to power. Anakin’s technical skill + aug/raw power are what define his skill, and those two elements define Vader’s skill as well. Since I’ve established that the quote does indeed refer to AOTC, we can determine from it that Vader’s raw power is equivalent (if not less than) the raw power that AOTC Anakin possesses. Hell I can even be generous and say his raw power is on par with that of a “flash of brilliance” AOTC Anakin. But we’ve seen how both of those fights go--not a very good outcome for Vader, really.
Except the quote’s explicitly referring to something OOU. It’s declaring that audiences will perceiveLuke as “not that powerful” compared to one such as AOTC Yoda, for example. It’s a declaration of intent, to start. It’s a quote that has backing in several sources, such as the ones below:
Until the Prequels, the only Jedi we’d seen in combat were old men and an inexperienced youth… and clearly, we hadn’t seen anything.
These quotes also back up some of my earlier claims. Lucas claims that Ben’s a “very old Jedi who was ready to go”, and that Luke is “semi-trained” and never gets the “full training”. He also is not regarded as a real Jedi, as we’ve never seen a “real Jedi doing what real Jedi do”. The second quote reaffirms the idea Ben’s a bad combatant by claiming that all he’s just an “old man” and Luke is an “inexperienced youth”, and claims “we hadn’t seen anything”, meaning that in comparison to the PT Jedi (such as Jinn, Kenobi’s PT iterations, Anakin’s PT iterations, Windu, Yoda’s PT iterations, etc), the OT Jedi (Luke and Ben) are shit.
The third statement claims the Jedi and Sith are “at the top of their game”, showing an implication that these Jedi are better combatants than the Jedi we’d seen in the OT, something that seems to be corroborated by the final statement, where Gillard states that some of the PT characters are “real master swordsmen” and they are “better than anything we’ve seen so far”, meaning that said PT combatants (cough, Dooku, cough) are much better than all the OT combatants we’ve seen (cough, Vader, cough).
First of all your argument hinges on the idea that Vader’s growth was predicated around that single boost he receives at the end of the novel. I showed sufficient evidence that he goes from being barely able to walk around to being faster and more nimble than before and I cited his boost at the end to lead into another point where sidious says:
Now that Vader had begun to tap deeply into the power of the dark side, his true apprenticeship could begin
The entire point of this part of the post was to explain that Vader overcame severe handicaps and grew considerably in all his abilities, going from being a walking pile of burnt garbage to someone whose “true apprenticeship could begin” by the end. All of those points lend to the idea he could grow at a rapid rate in the future. The post in itself referenced his boost yes, but it was designed to show you what kind of improvements the hindered version of the Dark Lord can make, now imagine what a “true apprentice” can accomplish in twenty years. As for the Padawan point, you provided no evidence for it so I don’t feel the need to respond. Until you cite Dark Times Vader growing more than he did the rest of his life, the point is moot.
No, my argument does not hinge on the idea that Vader’s growth was predicated around that single boost. The boost is not representative of his average annual growth. If somebody gains a massive power boost, we can’t apply that to their normal growth. We see Jacen Solo in Legacy of the Force: Sacrifice gains a massive sacrificial power boost from killing Mara Jade. He doesn’t gain these massive power boosts every day, not every week, nor every month. Likewise Anakin gains a massive power boost by jumping to the DS. Yet he isn’t going to be gaining boosts akin to that every other day or so, had he survived.
Likewise, Vader’s killing of Roan Shryne “firm[ed]” Vader’s faith in “the power of the dark side”. You haven’t provided evidence for why Vader going from, as you’ve said “a walking pile of burn garbage” to one whose “true apprenticeship could begin” is representative of normal growth. It’s evidently indicative of a massive boost in power. As for my point about Vader’s growth, it doesn’t require a citation, as I’m appealing to common sense. We see masters as they grow closer and closer to achieving their potential stagnating. Yoda says that he used to be able to lift 5 Muntuur stones, now (around pre-TPM iirc) he’s only able to lift 4. Vader hasn’t achieved nearly as much of his (revamped) suited potential in 19 BBY as he has in 10 BBY, so logically he’ll grow more when he has more of his potential to achieve than less, evident by my Padawan analogy.
So, to start with you cite the examples of Anakin and Kenobi growing at different rates. It’s really telling to me that you are using the literal Chosen One and Kenobi as your example for inconsistencies in growth. As for your point about the ragdoll gap argument it is a classic case of the argument of incredulity. You have provided no evidence or arguments to the contrary other than saying my thought process is “insane” and so the point still stands.
Except I wasn’t comparing Anakin to Obi-Wan at all. I literally pointed out two periods of their lives and compared the growth there to another period in their lives. I compared Anakin’s TPM-AOTC Growth to his AOTC-ROTS growth and stated that he grew more during the latter period than the former. I likewise compared Kenobi’s growth in the two time periods. Given that both of the characters’ growth is not linear, it’s logical to proclaim that all growth isn’t linear. Other examples of growths that aren’t linear is Sidious’ from TPM to ROTS compared to ROTJ to DE, therefore showing that there’s no validity in claiming linear growth.
My statements of incredulity were in regards to the fact that Vader’s growth being linear is completely unfounded and that Luke’s 19 ragdoll gap superiority to Shryne, to be quite frank, is utter bull. Tell me ISV, if Vader grows a ragdoll gap a year, why does he struggle with Ben Kenobi? Consider that under your premise of Vader >> ESB Luke > Ben ~ ROTS Kenobi ~ Dooku that you fail to account for AOTC Anakin. Anakin is a greater prodigy with 10 years of formal training, as a sharp contrast to Luke being a lesser prodigy with only 7 months (as you’ve cited later on in your post) of informal training. Logically then, given Anakin has a greater potential than Luke, he is more powerful than Luke. Dooku dismisses Anakin during one of his “flashes of brilliance”, times when Anakin performs at a far, far better state than his normal one. Thus making it evident of Dooku’s (vast) superiority to ESB Luke. Lucas also indicates that Luke’s training is subpar comparative to a normal Jedi in the following quote:
Star Wars Featurette: The Birth of the Lightsaber wrote:“In every episode from 4, 5, and 6, I kept improving the sword fighting because the assumption was that Luke was getting to be a better fighter, he was learning more, but at the same time he still wasn’t being trained as an original Jedi would have been trained.”
Okay forgive me I have not seen this source before, the date on the tweet says 2019. It would be reasonable to assume this is Chee referring to Canon Vader no? As for the surrender point, all sources including the film make it clear Ben gave up. Redundant evidence is redundant, next?
Okay so you decided to use the 6,4,2 argument lovely. Let’s take a look at the quote:
The idea of Vader using telekinetic powers during his fight with Luke was created during story meetings. There was concern, however, that the audience might think back to the first film and wonder why Vader didn't use all his powers on Ben; but this was easily explained by the fact that Ben was probably stronger than Vader. George Lucas and Leigh Brackett also discussed the different levels of the Force; maybe Ben was a six, Vader was a four, Luke is now at level two.
--Star Wars: The Annotated Screenplays
So, the determining factors for it not really holding authority are threefold:
1: This is a storyboard pitch meeting, where the executives come together to iron out power levels, so the “easy explanation” as that quote says is that Vader is less powerful than Ben, this is ambiguous however because of it’s terminology, which leads to my next point…
2: The words “probably” and “maybe” denote uncertainty in the “easy explanation” devised in the meetings. If Ben is “probably” stronger than Vader, that’s wonderful. It means there is a chance to assume as much, but it doesn’t mean it can be used as a concrete basis for scaling Ben off Vader.
3: The meetings took place back during the production of Empire Strikes Back as such they cannot be used as determining factors of the power levels of the characters now as opinions change overtime. For instance, Vader legitimately wins the duel as of 1977 in the Star Wars novelisation, yet we know from this screenplay that the writers think Ben is a 6 and Vader is a 4 around the 80s, so the veracity of such an old source can be called into question.
None of them actually make it clear that Ben gave up. I’ve always been of the opinion that he’s thrown the fight, something that the DK book quote makes evident. As for your point on Chee, the tweet is in response to a question about the 6, 4, 2 quote. Meaning that this is supporting evidence that the 6, 4, 2 argument stands. Chee follows Lucas’ lead on this, and declares that Obi Wan is indeed stronger than Vader, but power levels (raw power a force wielder can use) aren’t the only factor in a fight.
As for your arguments on the quote’s validity, the first two revolve around the core idea that the terminology “maybe” and “probably” are ambiguous, and that it makes no sense to declare that Ben > Vader solely on these quotes. Yet the general idea is that Chee’s quote allows reconciliation of the idea Ben > Vader. We see how his tweet was in response to a question about the quote, where he goes along with Lucas’ intent and declares Ben > Vader in raw power is canonically fact.
Okay, so I’m not sure how you got that out of the quote, I can post again:
“You have been learning, you’re young and quick, you offer me better sport than the old man.”
The argument can be made that this refers to speed since he cites Luke’s youth and speed as the reason he considers him “better sport” but overall speed kills in a lightsaber duel. To say that Luke is as technically masterful as Ben would be a stretch, but his “unparalleled learning in battle” and mimicry of Vader’s own hybridized form after minimal training lends itself to his raw threat level. So, my case still stands strong as ever in fact. Since you indicate that Luke is indeed faster and more mobile, the speed comparisons with Kenobi still work and if Dooku can’t produce a greater speed than the one I already cited, doesn’t that give Vader an advantage?
Furthermore your source is Google and even in the quote you gave, it mentions “physical exertion and skill” being a part of sport’s definition.
Here is an alternative interpretation from the Cambridge dictionary:
a game , competition , or similar activity , done for enjoyment or as a job , that takes physical effort and skill and is played or done by following particular rules
I don’t see how you attempt to invalidate the statement by citing the definition of sport. In this case (as seen in Shadows of the Empire as well) wouldn’t Vader’s enjoyment of fighting luke be based on how much a challenge is presented? Wouldn’t that indicate he poses a higher threat than “the old man?” If anything your definition of sport helps my case, since it implies that in this “athletic activity” Luke has greater “physical effort” and “skill.”
Which is all fair, but being a better combatant than somebody isn’t being more powerful than them. Ben’s an old man, so while his raw power is still at the level of Vader, his combatative skill is, to be quite frank, shit. To contrast, Luke lacks the raw power that Obi-Wan has, but he’s young, so naturally he’s more mobile than a man nearing the age of 60.
Here however, you try to claim that Luke’s mobility and greater speed are evidence of why he’s faster and more powerful than Ben. The double standards here astound me. You yourself claim that Luke’s greater speed than Ben shows superiority, but when I cite Dooku moving so fast that Kenobi is incapable of throwing up a defense to block his attacks, you claim that it’s an incorrect comparison? Here, I actually have to point out a glaring flaw with your entire logic, namely Vader’s linear ragdoll gap growth. According to you, Vader grows a ragdoll gap each year, meaning he’s jumped 3 from ANH to ESB, and Luke being outside his ragdoll range means that he’s at least a single ragdoll gap above Ben Kenobi, whom you claim is ~ ROTS Kenobi and therefore ~ Dooku. Yet not even Darth Sidious or Yoda are capable of ragdolling Dooku or Obi-Wan. In fact, Yoda is incapable of doing this to the degree that he’s forced to fight Dooku and push him back “slowly”. Somehow Vader as of ROTJ is a ragdoll gap above the likes of Yoda and Darth Sidious? That’s a completely insane argument, even by your standards. For one, Lucas himself explicitly states Vader in his suit could never become as powerful as Sidious was. He explicitly claims Vader can only become “80%” of Sidious. And that’s Vader’s suited potential, not his actualized power as of Return of the Jedi.
Vader also believes he can hunt Yoda down and kill him at the time of A New Hope:
Most of the Jedi had been destroyed. Some of the few who mattered the most, however, had not. Some had escaped, among them Yoda. This was disturbing. Old as the green little imp with the querulous voice was, he could still be a threat. - But be all that as it might, there was no Yoda, no Mace Windu leading this insurgency . . . no one who shone so brightly in the Force that Vader could not miss him. Whatever few Jedi might be left in the galaxy had nothing to do with this latest attack. -
...
Vader knew all about midi-Chlorians, of course-he personally had the highest count per cell ever recorded, more than twenty thousand. More than Yoda, and, he knew, more than his erstwhile Master, Kenobi. Which meant that, potentially, he could have a stronger connection to the Force than anyone. Since most, if not all, of the Jedi were no more, that was all the sweeter, though Vader was convinced that Obi-Wan had remained hidden all these years, as had Yoda, assuming the latter had not finally shuffled off into death. Yoda had been very old, after all, and the defeat and deaths of the Jedi could not have helped him age any easier. He could be dead. But it was unwise to make such assumptions about such a powerful Jedi Master.
…
"More important, though, was the knowledge that Vader's nemesis still lived. He would have felt it through the Force if the old man had died, of that he was certain. And this was a good thing, a very good thing indeed. Because someday, somehow, Obi-Wan Kenobi would pay for what he had done to Anakin Skywalker, and it would be Darth Vader who collected the toll. He would strike down Kenobi as he had so many of his fellow Jedi, be they Masters, Knights, or Padawans. Eventually the inevitable would become reality, and the Jedi would be no more."
So, perhaps Vader’s opinion on Yoda is irrelevant. Even if it wasn’t there is still that last bit of the quote you have to counter:
Luke would join Darth Vader or die. It would be something to look forward to. That would be the duel of a lifetime. This wasn’t even exercise.
If Vader considers it the “duel of a lifetime” and specifically compares that to how easy things are for him now, he is basically saying that Luke will pose a greater challenge to him than anyone before.
Another thing is that you didn’t address my other quote so I assume you concede? I’ll provide an explanation:
The quote says “At last” referencing all opponents before, that Vader in his ESB iteration found an opponent worthy of him. The quote specifically notes that it is Luke’s “swift” lightsaber skill and “power” in the force that make him worthy.
Points all still stand.
I was referring to ROTS Yoda. Whether Vader can or cannot defeat Yoda as of ANH (which I highly doubt, and it’s completely irrelevant anyway) is something I doubt we need to debate here. If Luke > all Jedi before that Vader’s met, that’s evidently including Windu, ROTS Kenobi, Yoda, etc, and the claim that ESB Luke > Yoda is something that’s easily refutable, namely through Lucas’ comments on it.
The quote clearly referring to Vader in his suited iteration means Luke is a greater combatant than Ben, but nothing in regards to their raw power with the force.
Star Wars in 100 Scenes wrote:Slowed by age, Obi-Wan is not the duelist he once was.
Meaning that Kenobi’s old age makes him a far slower duelist. One’s overall skill is a mix of raw power and technical skill, raw power affecting your augmentation and overall combat performance. Kenobi is explicitly “not the duelist he once was”, indicating a great disparity between his ROTS and ANH iterations. His ability in the force has diminished, as has his technical skill, leaving him a far worse combatant than usual.
Section II - Dooku Ragdolls
Extremely exhausted you say? From my recollection he “summoned power from throughout the universe” and then used a “whipcrack” of that power to incapacitate an unexpecting Kenobi. As for “the master of soresu getting embarrassed by Dooku” This is highlighted in the JN once again:
He can’t fight in two directions at once, Obi-Wan thought as he came up behind the Count. If we can —
Kenobi thinks Dooku is preoccupied with Anakin, so he is basically thinking: “all right, i’ll rush this guy while his back is turned.” The problem is that Dooku is aware of Kenobi and exploits that tactical blunder and by the time Kenobi can muster his defenses the choke has weakened him to the point he cannot fight back. Now yes, Dooku moves fast enough to catch Kenobi off guard but bursts of speed in equals are not uncommon. All you are proving is that Dooku is relevant to Kenobi, to which I agree, but speed also doesn’t denote anything in this instance, since it’s Kenobi’s tactical failing not his skill that ends up getting him incapacitated.
Obi-Wan is surprised that Dooku can hit him, yes, but that’s not refuting my argument. If Dooku is capable of taking the master of a completely defensive style off guard and then taking him out, then why can he not do the same to Vader? Vader’s style “lacks the polish of lifelong masters”. He lacks the technical refinement that all “lifelong masters”, such as Kenobi, Windu, Dooku, Yoda, etc have. Again the double standards. Why is speed not denoting anything? Your entire argument for Ben < ESB Luke revolves around the central premise that he’s faster and more mobile than him, so he has more strength in the force through a speed comparison. Given that this is an active combat situation, perhaps Kenobi is off-guard, yes, but that doesn’t change the fact that before he can so much as react, we see Dooku move so quickly that Kenobi cannot counter his attack. If you can make speed comparisons, you have to deal with them too. This is no “burst of speed in equals”, as you claim. Dooku’s capable of fighting at this level against two high level foes, Anakin and Obi-Wan at the same time. Consider that if there’s a duo and both of them stand a chance at soloing, then there’s going to be an immense stomp happening. That clearly doesn’t happen here. You cite Kenobi “stonewalling” Dooku earlier in your first post, yet Dooku’s caught utterly by surprise at Kenobi’s rapid change in form. Just months from ROTS, Windu fights Dooku, and Windu attempts to strike Dooku down. Dooku seems to easily deflect the blow and mocks Windu to his face about it. Likewise Dooku is able to take blows from Yoda himself on Vjun, and is only pushed back “slowly”, while taunting Yoda the entire time. In AOTC Dooku and Yoda fight in a relatively close fight, with an exhausted Dooku managing to exhaust Yoda (I’ll cite that in my rebuttal). We then see that Dooku is capable of contending and practically beating Yoda in 20 BBY in the comic Yoda Uncovered.
We clearly see here that he contends with Yoda in bladelock, then Yoda jumps away and attempts to flip over Dooku, but Dooku blasts him away with lightning. This is an undeniable showing of nigh-parity. If Dooku, as you claim, is extremely far beneath Yoda per the tiering system, then why is he able to perform this well? Is it because perhaps Dooku is not so weak that he would be stomped by his master of by Yoda? As you claim, maybe Dooku doesn’t have raw power on par with the PT titans, or even near them (I’m not claiming this is true, to clarify). But even if this is true, Dooku’s ability to contend with foes with (as you claim) far greater raw power than him is an undeniable advantage he has. Vader just hasn’t shown the ability to compete with a tier 9 fighter like Yoda the way Dooku has. Dooku has been able to resist Yoda’s offensive onslaught and leave his former master exhausted for it all those times. To contrast, Vader has low showings against fodder like a post-prime An’ya Kuro
[....]
Should we consider Darth Vader, a character that has unfavorable showings against fodder like Kuro to be a top tier? Should we consider Vader, somebody that’s shown time and time again his utter incompetence when dealing with powerful foes to be on par with a master such as Dooku? Should the character holistically portrayed to be with the likes of TPM Maul, or even TPM Kenobi be considered for superiority to somebody that gave Yoda the fight of his life several times and practically beat him once?
Now I am truly lost. I give you evidence that Kenobi was distracted at the time and didn’t throw his barrier up as supported by the Junior Novel which reads: He reached for the Force to counter Dooku, but the attack had been too sudden. This is not an arguable point, whether Kenobi’s reactions are “almost impossible” to take by surprise means nothing. That word almost in your quote, that refers to a margin of time where he can be taken by surprise, and that is what happened by all accounts that I have shown...
The attack had been too sudden, yes. But this is active combat, there is a time Kenobi can be taken by surprise, but the fact that Dooku’s able to do so means that he’s able to engineer and exploit openings in others’ defenses, something that Vader will inevitably fall to. We see in Vader’s duels with Luke during ESB and ROTJ that he is prone to utilizing long, sweeping strikes. Dooku can easily take advantage of this, the example being his fight with Kenobi in ROTS, where he’s able to easily take Kenobi out by exploiting the openings he leaves. Vader’s somebody that has been countered by a lesser prodigy than Anakin in Luke during ESB, even being injured in it.
Expanding on Dooku’s superiority to Kenobi:
https://www.youtube.com/watch?v=OcXaicGvcvA
In the link above, Dooku fights both Kenobi and Skywalker evenly (if not holding an advantage) for a period of over a minute. At approximately 1:01, we see Dooku remove Kenobi from the fight with ease for a time. Throughout we also see Dooku’s ability to fight with great mobility, something that gives him an undeniable advantage against Vader’s restricted mobility. At around 2:04, we see Dooku utilize a force blast that knocks back both Anakin and Obi-Wan, pushing them to their knees. Given the disproportionate strength of a barrier and the fact that both Kenobi and Skywalker had them up at the time, we can conclude that Dooku’s superiority to Kenobi is all but fact. Then we see Dooku overpowering Kenobi’s superior in Anakin in bladelock at 2:52.
As for Revenge of the Sith itself, we see numerous times in the fight Dooku’s evident superiority to Kenobi:
Revenge of the Sith wrote:Anakin launched himself at Dooku’s back and the count half turned, gesturing casually while holding Obi-Wan at bay with an elegant one-handed bind.
Dooku is able to casually throw chairs at Anakin while the latter charges at Dooku, simultaneously holding Kenobi at bay one-handedly. Consider that Dooku shows seemingly no strain throughout, and is able to counter Kenobi while utilizing the force to throw stuff at Anakin.
Revenge of the Sith wrote:
While effortlessly deflecting a rain of blue-streaking cuts from Kenobi
Dooku’s able to “effortlessly” counter Obi-Wan’s attacks, another showing of superiority.
You claim that the “whipcrack” of energy ragdoll and the ragdoll shown in the movie where Dooku kicks Anakin back and then chokes Kenobi are the same. Yet this is evidently not the case. The scene in question, where Kenobi attempts to double-team Dooku and gets caught off-guard is depicted after Dooku flings Kenobi across the room effortlessly.
Revenge of the Sith wrote:Before the pieces could even hit the floor Dooku was in motion, landing a spinning side-stamp that folded Skywalker in half; he used his last burst of dark power [....] knocking the Jedi master back down the stairs.
This part specifically is where Kenobi is removed from the fight, similar to the section of the JN you cited. The part that Dooku flings Kenobi away with a “whipcrack” of power is earlier on, and is depicted in the film as Dooku pushing Obi-Wan, not choking him. There’s no evidence that Kenobi is caught by surprise when flung across the room by surprise the first time, and while it’s certainly possible that he only had a passive barrier up, Dooku still effortlessly chucks him away, and since there’s no evidence to the contrary, I can attribute this to Dooku’s own skill and power being greater than that of Kenobi’s.
Here’s the clip showing specifically what I was referencing:
https://www.youtube.com/watch?v=eYT3ctPuVRw (1:28).
The quote from the ROTS JN you provided states that Kenobi was caught off guard when Dooku choked him, but that’s clearly not what Stover references during the “ragdoll” sequence of his novel.
So, you are saying that speed is the defining factor here, and force augmentation somehow correlates to a massive gap between the two? A quick burst of speed on an unexpecting Kenobi proves nothing. If you want to cite reactionary times for unsuspecting opponents as a determining factor let me point you to Cade Skywalker and Darth Krayt:
Except there’s no evidence that Kenobi was caught by surprise and there’s no evidence that this was merely a quick burst of speed as opposed to Dooku having just that much better augmentative capability than Kenobi does. You mention how barriers are easy to throw up in your Krayt comparison, but Cade isn’t using TK on Krayt then, he completely catches Krayt by surprise and takes him out with a saber attack. To contrast, Dooku augments himself sufficiently that Kenobi isn’t given the option to react in the example I’ve cited.
1: Dooku could not break Kenobi’s guard and it was too “bewilderingly fast” for him to “dare strike” meaning they are relative.
2: Dooku could not break Kenobi’s defenses on a whim and needed a defensive lapse as supported by the junior novelization.
3: Speed does not denote any form of parity if the opponent was caught off-guard.
Points still stand.
1. Dooku’s ability to counter attacks from Mace Windu a few months before ROTS with ease and nearly stalemate Yoda on several occasions, combined with the fact that Dooku is caught off-guard by Kenobi and Anakin’s change in form from Shii-Cho/Ataru to Soresu and Shien to Djem So respectively shows your argument is wrong.
2. While Kenobi may not have had an active barrier up, he certainly had a passive barrier up given the situation is in active combat, and as we’re speaking of two separate incidents within the fight, it’s safe to say that Kenobi wasn’t necessarily caught off-guard/by surprise.
3. Yet Kenobi wasn’t caught off-guard by Dooku’s assault, there’s no evidence saying he was. Dooku is able to augment himself so much that Kenobi is unable to defend himself and is flung across the room.
So sure, Anakin doesn’t have the clarity of mind at this point that Kenobi does, but any huge benefits to rationality are overridden when he’s just taken “Force LSD” and “jumped to a level nine.” What the quote is saying is that Anakin is being an idiot and isn’t good at decision making or as highlighted in the last two quotes above when Kenobi exploits this weakness on the ridge at mustafar. This does not mean he is any slower or less skilled than he was previously.
Furthermore their parity is noted by Kenobi being able to “deflect his force blasts”:
Obi-Wan backflipped from the conduit to a coupling nexus of the main collection plant; when Anakin flew in pursuit, Obi-Wan leapt again. They spun and whirled throughout its levels, up its stairs, and across its platforms; they battled out onto the collection panels over which the cascades of lava poured, and Obi-Wan, out on the edge of the collection panel, hunching under a curve of durasteel that splashed aside gouts of lava, deflecting Force blasts and countering strikes from this creature of rage that had been his best friend, suddenly comprehended an unexpectedly profound truth.Star Wars: Episode III - Revenge of the Sith novelization
The argument can even be made that most of the fight Kenobi is “holding back” somewhat, it is only when he “let go” that he can defeat Anakin:
But that’s not really true, Obi-Wan thought as he ducked and wove and parried. Both he and Anakin felt the anguish of their need to kill the other. But Anakin had turned to the dark side, and despair and pain strengthened the dark side. It gave him an advantage Obi-Wan could not match. Unless he let go of his own despair and let the living Force move him — the Force that bound all living things together, even Obi-Wan and this new, deadly, evil Anakin.Star Wars: Episode III - Revenge of the Sith junior novelization
Which is supported by The Ultimate Visual Guide:
So no Kenobi fought Skywalker as an equal and possibly even became his superior at the end, that is the most supported interpretation.
Kenobi being able to deflect force blasts is not a showing of parity whatsoever. Kenobi’s barrier allows him to do so. In the Gillardian tiering system you cite, Kenobi is explicitly an “8”. It’s completely false to claim that Kenobi magically jumps to a 9 on Mustafar. Gillard uses “Obi Wan is an 8” as a blanket statement encompassing ROTS. Consider that Kenobi and Anakin both have intimate knowledge of each other’s forms, and while this link goes both ways, Kenobi benefits moreso from it than Anakin, as Anakin’s gone essentially batshit in this fight, and Kenobi being a defensive fighter gains more of an advantage the whole fight if he knows what his opponent’s next move will be. Considering that Kenobi also gives ground the whole fight, it’s pretty obvious that Anakin holds an upper hand… until he makes a fatal blunder.
The quote states the two are shadows of their former selves, then it immediately says “neither has fought another lightsaber-wielder for many years.” Which leads us towards the idea the quote is referencing dueling abilities, not power in the force. It would also be completely arbitrary to include something about force abilities in an article discussing respective styles of combat during A New Hope. Of course Vader’s skills being a shadow of his former self doesn’t really hurt my argument, since that exact same source states Vader grows “far more formidable” during the 3 year interrim between A New Hope and Empire Strikes Back. That idea is affirmed by Luke being Vader’s greatest challenger, and specifically cited as Ben’s superior.
And the quote referencing their duelling abilities was my point. Considering that dueling abilities are related to 2 things, augmentation and technical skill. Augmentation is directly related to one’s raw power in the force, and therefore since Kenobi’s skill as a duelist has regressed, his force power has likewise. Since you’ve not responded to my claim that Vader’s comment that “your powers are weak, old man”, means that Kenobi’s powers have regressed since ROTS, I’ll take that as a concession.
This mindset isn’t the same when he faces Vader. On Bespin he thinks he can beat Vader, this is evident in the film with the line “you’ll find i’m full of surprises” and in other sources saying “Luke was far too hasty” or “luke thought he he was ready to face Vader, he couldn’t have been more wrong.” So during this duel he would be more confident in his abilities and thus he is able to access more power.
Except Luke makes an earnest attempt at lifting the X-Wing and fails utterly. His confidence or lack thereof in his abilities doesn’t change the fact that this kind of TK is something he deems beyond himself with good cause--he simply cannot do so.
So, a giant sith crystal used in Sithisis to conduct galactic scale rituals by Darth Sidious himself, a reservoir of Darkside crystals and gadgetry that will “help Lord Vader recover”, sith weapons stored around the gallery, and the final piece an enormous Holocron recovered from Korriban itself.
It should not be hard to see why this massive complex would remind Ferus of Korriban. So yes Dooku is amped and there is no reason to assume he outgrew this nexus.
Characters grow only through conflict, per Kreia. Considering that Dooku is involved in a massive galactic scale war, it’s pretty obvious that he grows a lot. Consider also that Dooku throws the ships and cruiser “with ease”. My comparison was simple, that Dooku’s TK is far, far beyond ESB Luke’s. Dooku being able to casually throw around cruisers (while amped, yes) and then undergoing 3 years of immense growth is a testament to his power. You haven’t sufficiently demonstrated that the nexus of Korriban circa 22 BBY is strong enough that it means Dooku cannot throw cruisers around when not amped by it. Perhaps when not amped by Korriban Dooku won’t be throwing ships around with such casual ease. My point remains however, that Dooku’s TK is demonstrably far beyond what Luke as of ESB has shown.
Sure, Anakin has flashes of brilliance, but Dooku’s skills aren’t even really put to the test until he duels Yoda:
Meaning that he capitulated in some fashion hence the word “toying” that I used. He still got tired.
To put (someone or something) to the test is defined as “to cause (someone or something) to be in a situation that shows how strong, good, etc., that person or thing really is”. Meaning that Yoda is the only one thus far that has shown how strong Dooku really is. That doesn’t mean Anakin couldn’t have pressed him though. Toying with one explicitly means that you’re playing around with them to amuse yourself. Dooku is pressed by Anakin to a degree, but it isn’t something that makes Dooku utilize his full ability.
You didn’t provide evidence for it though. I am going to need to see proof Dooku can exhaust AOTC Yoda, not sure how that is relevant to my arguments though.
I didn’t forget anything. Augmentation isn’t factored into the quote, Vader’s “feats” of strength are what were referenced in Dark Lord: The Rise of Darth Vader it’s not Vader saying his cyborg limbs are stronger than his flesh and blood, but rather the “feats of strength” he can accomplish “distinguish him from Anakin” which is specifically likened to how Anakin once had limited access to the Temple archives but now has all of that data to view at his fingertips from anywhere in the galaxy. So even if Anakin was vastly superior to Vader in the force which would make him logically stronger than Vader, that isn’t what the quote is referencing. It’s also not hard to believe that Vader’s cybernetics and augmentations with the force could supersede Anakin’s own strength when you consider what enhancements he received:
And I see no reason for said feats of strength to be referring to raw power in the force. Like, we clearly see Anakin being far superior to Vader in terms of the force, and there’s no reason that Vader’s cybernetic enhancements should make up that gap. Your argument that Vader jumps a ragdoll gap a year clearly falls flat when we take into account the fact that if in 19 BBY, Vader with aug + cybernetics > Anakin with Aug, then by 4 BBY, he should be tossing around the PT Titans with ease.
The quote says that Vader has an enhanced version of Grievous's own cybernetics and we know the quote doesn’t mean speed or life support systems since those two things are very different for Grievous and Vader respectively. For reference to Grievous:
As Mace already knew from Ki-Adi-Mundi and Shaak Ti, Grievous was well trained in the Jedi arts. He could recognize the hand of Dooku in the general's training and technique. His strikes were as forceful as any Mace had ever had to counter, and his speed was astonishing.
-Labyrinth of Evil
Who has Mace Windu fought before this point? Ah yes, Dooku himself.
If Vader was say half of Anakin in power at this point, even something as low as 20 percent, it’s easy to see why his augmented cybernetics would be beyond Anakin’s base strength if he is already packing Grievous's without augmentation.
Also the Return of the Jedi: comic I used in the opener wasn’t countered, so I assume you conceded that point?
For your point about Mace fighting Dooku: it’s fairly evident from how short the fight is (literally one or two exchanges) that Mace can’t get a feel for Dooku’s strength from it. Considering Dooku’s fought on par with the likes of Yoda and not yielded in bladelock, your claim that Vader can physically overpower Dooku when Vader’s already shown himself to be much weaker than Yoda is incorrect. Considering that I've given and backed up evidence for why Vader <= AOTC Anakin, I think it's safe to say that no, Vader isn't striking with "more deadly invincibility" in that comic.
Section III - Parity to Yoda, Reaffirmed
This doesn’t say “above” Yoda at all, it merely says as strong as Yoda at best.
Well yes, but it’s showing that he’s at least ~ Yoda, something that other sources show as well.
A stretch to say the least. Caedus didn’t even know Anakin, he would be going off records and what little Luke could tell him, not a very reliable source.
Have you read Bloodlines? Caedus flow-walked into the past. He basically time-travelled, to be concise. He isn’t going off of old records and what Luke could tell him, evident from Caedus witnessing a scene that there is likely no record of--Anakin being denied mastery.
Potential does not correlate to actualized power, Luke has the potential to be what Anakin could have been per Lucas, yet i’m sure you would disagree he was equal to Anakin as of Return of the Jedi.
Except this isn’t referring to Anakin’s potential whatsoever. Sidious didn’t say “Anakin has the potential to be stronger than myself”. Sidious says that as of that minute, Anakin is possibly stronger than himself.
The novelisation describes this as a complete stomp and you haven’t cited a reason why Anakin would be > Yoda to begin with. According to Gillard Anakin starts Revenge of the Sith as an 8, he can’t be more powerful than Yoda if he’s literally a tier below him.
Gillard isn’t the only thing that supports Yoda being more powerful though:
Where does Gillard ever claim Anakin starts ROTS as an 8?
"Hayden Christensen is one of the best there is," says Gillard. "I've seen hundreds of sword fighters, people who do it for a living, and he leaves them all in his wake. His style has changed a bit since Episode II, when he was only a level seven. On this he's a level nine."
Alright, so basically we know Yoda can’t have been actively using it like Dooku was, this is for a few reasons. The first being that we know from this little email and Dooku himself, if Yoda ever turned to the Darkside he would “annihilate sidious” and according to Yoda he could “fall on him like a thunderbolt and annihilate Dooku utterly.” So, if Yoda gave into the darkside and actively drew off of it like you imply, he would have blitzed and stomped Dooku. According to the author who confirms Dooku was right and from Dooku himself. So what we have now is a Yoda who might be drawing off of a seemingly dual nexus (which means Dooku would be double amped.)
Or and far more likely, Yoda is drawing off of Vjun which is a specifically darkside nexus but remains in the light as we know he can’t fully embrace it. This means Yoda would be essentially conflicted which as noted by Vader “poisons the darkside” so Yoda’s power and the darkness would be fighting each other leaving Yoda either slightly weakened or at base level power-wise.
All of this means nothing unless you can prove the idea that Tyranus is supremely above Kenobi anyway (which you have failed to do.)
Yoda is actively drawing upon the dark side throughout this fight. It’s pretty evident in the book itself. “In the dark, drunken Vjun air, Yoda was terrible to behold”. “And yet, even here on Vjun, where the dark
side whispers and whispers to me...love you enough to destroy you I do”.
Yoda utilizing the dark side doesn’t mean that he’d be hindered or conflicted. There’s nothing that actually hints at conflict. Yoda states he’s going to kill Dooku, and that the DS “whispers and whispers” to him. Given that you’re using the author quote over there, I think that means that you really won’t object to my use of it as well. And Stewart explicitly states, “so my instinct would be that he’s tapped into Vjun”, and that “Yoda and Dooku are both like surfers in a place with big waves. The more expert the surfer, the more they can do with that power”. Meaning that Yoda is utilizing the nexus of Vjun to a greater effect than Dooku is, but he’s only pushing him back, “slowly, slowly”.
You baselessly assume this refers to Attack of the Clones Anakin when Revenge of the Sith was already in production and was mostly completed:
Except Revenge of the Sith wasn’t released yet. Until something is published (released in this scenario), it has no canonical validity. There’s a reason that Supernatural Encounters isn’t canon, it isn’t published. Meaning that by default, Hidalgo is referring to AOTC Anakin because Revenge of the Sith just doesn’t exist yet as a canonical entity.
There is no reason to assume it locks Vader under his AOTC iteration. Sure, Anakin is more skilled than Vader that doesn’t have anything to do with my argument. I made sure to be very careful when discussing Vader’s lightsaber techniques and I made an argument that Vader would pressure Dooku in different ways than Anakin, he is slower, more methodical. This would not be like the duel on the Invisible Hand, Dooku would break over a period of time, which I recall describing in the opener.
Well skill is directly related to power. Anakin’s technical skill + aug/raw power are what define his skill, and those two elements define Vader’s skill as well. Since I’ve established that the quote does indeed refer to AOTC, we can determine from it that Vader’s raw power is equivalent (if not less than) the raw power that AOTC Anakin possesses. Hell I can even be generous and say his raw power is on par with that of a “flash of brilliance” AOTC Anakin. But we’ve seen how both of those fights go--not a very good outcome for Vader, really.
I don’t blame you for this but the quote doesn’t work for what you are trying to make it do. DarthAnt66 posted this in his penultimate debate with Azronger and I’m guessing nobody ever bothered to go read the source it comes from?
The entire quote is talking about the audiences perceived reactions to the scene, nothing here is out of universe, it’s all about how moviegoers might have a new understanding of different scenes with the addition of the prequels.
Except the quote’s explicitly referring to something OOU. It’s declaring that audiences will perceiveLuke as “not that powerful” compared to one such as AOTC Yoda, for example. It’s a declaration of intent, to start. It’s a quote that has backing in several sources, such as the ones below:
“We will finally get to see Jedi do what Jedi were designed to do. In the first one, you had this very old Jedi who was ready to go, and one who had been reconstructed who was half human and half machine. The only other Jedi who comes along is Luke, who is sort of semi-trained by Yoda, but never really gets the full training. So you’ve never seen a real Jedi doing what the real Jedi do, until now.” - George Lucas
Until the Prequels, the only Jedi we’d seen in combat were old men and an inexperienced youth… and clearly, we hadn’t seen anything.
Star Wars Insider Magazine #131 wrote:Before this scene, the lightsaber battles we’d seen in the Star Wars movies involved older Jedi, or Jedi who were yet to become full-fledged Jedi Knights, but here we saw Jedi and Sith fighting when they were at the top of their game.
Starwars.com - Homing Beacon #57 wrote:"We're trying to go much more classical for some characters," says Gillard, "Some of the characters are real master swordsmen, better than anything we've seen so far. So we're using an old, classical European style for a couple of the characters." - Nick Gillard
These quotes also back up some of my earlier claims. Lucas claims that Ben’s a “very old Jedi who was ready to go”, and that Luke is “semi-trained” and never gets the “full training”. He also is not regarded as a real Jedi, as we’ve never seen a “real Jedi doing what real Jedi do”. The second quote reaffirms the idea Ben’s a bad combatant by claiming that all he’s just an “old man” and Luke is an “inexperienced youth”, and claims “we hadn’t seen anything”, meaning that in comparison to the PT Jedi (such as Jinn, Kenobi’s PT iterations, Anakin’s PT iterations, Windu, Yoda’s PT iterations, etc), the OT Jedi (Luke and Ben) are shit.
The third statement claims the Jedi and Sith are “at the top of their game”, showing an implication that these Jedi are better combatants than the Jedi we’d seen in the OT, something that seems to be corroborated by the final statement, where Gillard states that some of the PT characters are “real master swordsmen” and they are “better than anything we’ve seen so far”, meaning that said PT combatants (cough, Dooku, cough) are much better than all the OT combatants we’ve seen (cough, Vader, cough).
 IGLevel Four
IGLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 8:42 am
Section IV - Vader’s (Lack of) Advantages
Here I’m only citing this one part of your post because I’m not going to cite every small portion, but don’t take this as a concession, I’m countering every relevant part of that post.
While Barriers and Lightning can block lightning, it’s stated that Yoda deflected Dooku’s lightning “far from easily”. Dooku is capable of blasting Anakin back with his lightning while being held in a chokehold and in saberlock (link).
You also haven’t provided evidence for why SK’s lightning is on par with Dooku’s. Given Dooku’s capable of pressing Yoda with his lightning, there’s not really evidence for why SK’s lightning is that much better than his.
As I’ve already proven, Dooku is relativistic to a nonhindered version of Yoda, and he’s dismissing Kenobi with ease when not pressed by Skywalker simultaneously and/or in a state of stupor.
Dooku is definitely > a Kenobi that had ample opportunity to muster his defenses. I’ve sufficiently shown Ben’s inferiority to his ROTS iteration per a wealth of sources, including George Lucas himself. While Luke may have combatative skill above that of Ben, that doesn’t preclude having more raw power, and your “ragdoll gap a year jumping” argument doesn’t stand anymore.
No reason to believe it doesn’t refer to his AOTC iteration, so this is a baseless claim.
Luke may find the task impossible, but he also is incapable of doing so as well. Him not thinking he can do something doesn’t mean he automatically won’t be able to. Luke deems the task impossible because it is something he deems beyond his own abilities, something he should be an accurate gauge for at the time. You’ve yet to substantiate why Dooku’s amp isn’t mitigated by the fact that he’s capable of throwing the ships easily and war growth. To reiterate that argument, even if Dooku can’t throw the ships with ease after he has no nexus amp, he’ll still be able to throw them to some degree, if we account for war growth. To contrast, Luke has nothing putting him near that level of TK.
Dooku’s lightning is capable of giving Yoda difficulty. Given tutaminis is a better counter for lightning than a barrier (energy absorption vs using TK to create a protective bubble), it makes sense that Vader will be incapable of defending against lightning that’s pressing Vader’s vast superior in Yoda with a barrier, an inferior form of lightning defense than tutaminis. As for using a saber, I’ll be responding to that in my next section.
Section V - Dun Moch and Stamina
Ferus Olin bringing up Padme’s name to Vader makes Vader go batshit. Dooku has knowledge of Anakin’s “messy private life”, and therefore will have an ability to make Vader go into a rage, in which he will leave more openings that Dooku can exploit with ease, as Dooku’s shown himself quite proficient in that regard, through his ability to create openings in his fight with Kenobi and Skywalker and exploit them.
Dooku’s use of Dun Moch is evident in all of his fights--he taunts Kenobi as he toys with him in AOTC, taunts Anakin in AOTC, taunts Yoda in AOTC, taunts Windu as they fight, taunts Yoda in YDR, taunts Anakin in ROTS, etc. Vader’s form “lacks the polish of lifelong masters”--it’s sloppy in comparison. Dooku’s ability to contend and often overpower Anakin in bladelock as well as stalemate Yoda in bladelock two examples of how he can contend (if not overpower) Vader in a contest of aug. Dooku’s greater mobility and skill with telekinesis and lightning will allow him to exploit great openings in Vader’s enraged state.
You claimed in your first post that Dooku has terrible stamina, one of the most incorrect claims you’ve made through this SS.
Zannah claims that most duels end before a minute, and that “few duels lasted more”. “All-out combat was exhausting”, and Dooku engages in all-out combat with extremely powerful foes quite often. If you count the fight beginning as of the lightning exchange, Dooku fights Yoda (while exhausted) for a total of 80 seconds, whereas if you count the fight as only saber combat, it’s a 40 second long fight. Considering Dooku’s already tired and he’s capable of tiring Yoda in either an extremely long fight or an above average fight, I doubt this can be used to claim Dooku has bad stamina. Dooku duels Anakin and Obi-Wan together for a period of 40 seconds and then holds up against Zonakin for roughly the same amount of time. He duels two opponents that are extremely powerful individually, but together are a nigh-unstoppable duo for above average periods of time, then duels a Yoda+ opponent on his own for an above-average period of time. There’s no evidence for Dooku’s stamina really being that bad when he can contend with a duo of a character far inferior and reasonably superior, as well as an individual character marginally superior for above-average portions of time, leaving them exhausted as well.
Conclusion
Every point I’ve made still stands here. Dooku is far more powerful that ROTS Kenobi, who’s superior to his ANH iteration, who’s >= ESB Luke. Vader has power on par with likely his AOTC iteration, somebody that Dooku is far more powerful than. Dooku’s lightning is at a similar range of power to that of Galen Marek, evident from Dooku’s capability of pressing Yoda with it. Vader’s weakness to Dun Moch in a fight is something that will haunt him against Dooku, and Dooku’s stamina is top-notch. None of your points stand really, however. ESB Luke (by extension Vader) are not superior to ROTS Kenobi in any way, shape, or form. Dooku is far above ROTS Kenobi, and Dooku’s advantages are far greater than the limited advantages Vader possesses.
@ISV: Your turn
@EmperorCaedus @Cheth @BoD @”lorenzo.r.2nd” @Latham2000 @Syndiciate @MasterCilghal
(Tagged basically everybody who posted on thread).
Firstly, you haven’t established why “taking out powerful beings like Ventress with it” has any relevance to Vader whatsoever, beyond the fact that the Count can use it on a whim. Secondly, the example you cite is basically Jedi Ventress before she received any of the training from Dooku that makes her so formidable, she literally still has her Jedi lightsabers.
Here I’m only citing this one part of your post because I’m not going to cite every small portion, but don’t take this as a concession, I’m countering every relevant part of that post.
While Barriers and Lightning can block lightning, it’s stated that Yoda deflected Dooku’s lightning “far from easily”. Dooku is capable of blasting Anakin back with his lightning while being held in a chokehold and in saberlock (link).
You also haven’t provided evidence for why SK’s lightning is on par with Dooku’s. Given Dooku’s capable of pressing Yoda with his lightning, there’s not really evidence for why SK’s lightning is that much better than his.
Dooku is relativistic to a hindered version of Yoda, which means absolutely nothing since he is incapable of simply dismissing ROTS Kenobi which renders the entire feat moot to Vader.
As I’ve already proven, Dooku is relativistic to a nonhindered version of Yoda, and he’s dismissing Kenobi with ease when not pressed by Skywalker simultaneously and/or in a state of stupor.
Dooku can only ever be potentially > a Kenobi who can’t muster his defenses. With Ben I’m sure you could prove that, but you have failed on this occasion. That also has no relation to my Luke points which render the Ben fight far beneath peak Vader’s capabilities.
Dooku is definitely > a Kenobi that had ample opportunity to muster his defenses. I’ve sufficiently shown Ben’s inferiority to his ROTS iteration per a wealth of sources, including George Lucas himself. While Luke may have combatative skill above that of Ben, that doesn’t preclude having more raw power, and your “ragdoll gap a year jumping” argument doesn’t stand anymore.
No reason to assume the quote refers to his AOTC iteration so this is a baseless claim.
No reason to believe it doesn’t refer to his AOTC iteration, so this is a baseless claim.
Glad we agree that Luke “finds the task impossible” because that is why he is incapable of performing the feat not because he lacks the power to do so. Dooku is not “scarcely amped” and there is no evidence that you have presented implying he made up for his Korriban power difference over the Clone Wars.
Luke may find the task impossible, but he also is incapable of doing so as well. Him not thinking he can do something doesn’t mean he automatically won’t be able to. Luke deems the task impossible because it is something he deems beyond his own abilities, something he should be an accurate gauge for at the time. You’ve yet to substantiate why Dooku’s amp isn’t mitigated by the fact that he’s capable of throwing the ships easily and war growth. To reiterate that argument, even if Dooku can’t throw the ships with ease after he has no nexus amp, he’ll still be able to throw them to some degree, if we account for war growth. To contrast, Luke has nothing putting him near that level of TK.
The quotes you used only say that Vader is incapable of conjuring or defending against the power with his limbs, this doesn’t mean his force barrier or lightsaber would be insufficient, and even if one or two blasts got through, his insulation and armor minimize the damage that could be done. Furthermore, the only time lightning has slowed Vader at all, was against powerful masters of the force like Galen Marek or Darth Sidious himself, both characters that have no connections to Dooku that you have established in this debate.
Dooku’s lightning is capable of giving Yoda difficulty. Given tutaminis is a better counter for lightning than a barrier (energy absorption vs using TK to create a protective bubble), it makes sense that Vader will be incapable of defending against lightning that’s pressing Vader’s vast superior in Yoda with a barrier, an inferior form of lightning defense than tutaminis. As for using a saber, I’ll be responding to that in my next section.
Section V - Dun Moch and Stamina
Ferus Olin bringing up Padme’s name to Vader makes Vader go batshit. Dooku has knowledge of Anakin’s “messy private life”, and therefore will have an ability to make Vader go into a rage, in which he will leave more openings that Dooku can exploit with ease, as Dooku’s shown himself quite proficient in that regard, through his ability to create openings in his fight with Kenobi and Skywalker and exploit them.
The Last of the Jedi: Reckoning wrote:Ferus saw the glow of Vader's lightsaber as he activated his own.
This was it, then. The final confrontation.
He was ready. His rage was ice and fire.
He charged.
His first blow was easily parried. He came at Vader again. Again. Circling, jumping, vaulting past him, turning. Each time his lightsaber came toward him, it was eilher deflected in a shock that ran up his arm, Vader simply wasn't there.
"If you cannot even touch me, how can you win?" Darth Vader asked.
Ferus focused on his anger. He remembered Palpatine's words.
There is no limit to what you can do.
He charged at the dark figure again. This time his strike came close. He touched the edge of Vader's cape. He smelled the singed material.
Now, while he's off balance. Now.
"Maybe I'll just get lucky," Ferus said. "Anakin."
Vader came at him with surprising swiftness, but Ferus was able to Force-leap away. Still he sensed that Vader was holding himself back, playing with him for now.
"So you know who I was," Vader said. "Do you think that would make a difference to me? Anakin Skywalker is dead."
"Was it because the Council wouldn't let you become a Master? You always had to struggle with your ego, didn't you?"
"It was never a struggle. I was always the best."
" 'Best' is not a Jedi concept."
"That is the trouble with the Jedi."
Ferus wasn't tired yet, but he knew he was expending too much energy. He was tapping into his anger and fighting better than he ever had, but it wasn't enough. He had to unsettle Vader. He had to find the key.
He had everything he needed to defeat him, didn't he? He had the Sith Holocron for strength, Vader's true identity in his hand, his own rage. With those tools, he could do it. The Emperor had told him he could. Ferus thought quickly. He wanted to pick the battleground. Someplace that would unsettle the former Jedi.
There - the stairway to the Jedi High Council spire. Ferus started to climb. He knew Vader would follow.
He came out into the circular room. It was half rubble, the seating blackened lumps, the vast transparisteel shattered. Wind whipped through the room.
The Dark Lord entered. The wind blew back his cape. He stood, legs apart, ready for battle. Looking forward to it, Ferus was sure.
"The Emperor cannot protect you now," Vader said.
What next? What could Ferus do to get him off balance? He suddenly had a flash of intuition. He remembered what Keets had told him.
"What about Senator Amidala?" he asked, leaping away from Vader. He faced him, his lightsaber held in an offensive position. "What about Padme? What happened on Mustafar?"
He felt the quake in Vader. He had reached him at last.
"Do not mention her name!"
"I thought it was a lie, that the Jedi killed her," Ferus suddenly understood, the Sith Holocron burning under his tunic. "ft wasn't. You killed her, didn't you? You killed the woman you loved."
Vader's wrath filled the room. Ferus could feel it. Instead of turning away from it, he took it. He filled himself with it.
This is what the Emperor meant. This is the last step.
He flew across the room and this time he landed a blow.
Vader roared. It was a howl of fury, inarticulate, undisciplined. Totally unlike his usual icy control. The control box on his chest started to smoke.
Stones in the floor ripped out and were flung toward Ferus. He dodged them, rolling and twisting away. A blackened piece of furniture flew across the chamber and smashed into the wall over his head.
Anything that could be torn from the floor or walls came at him - conduits, debris, hunks of stone. He dodged and weaved, attacking and retreating as Vader hit him with everything he had.
"How did you kill her, Anakin? Did you lose control? Did you see her die, Anakin? Is that why you wanted Zan Arbor to perfect that drug? Was it for you, Anakin? So you could forget her? So you could forget your wife?"
Another roar from Vader. part of the ceiling gave way. Durasteel melted, smoke rose from the debris. Ferus leaped over a gaping hole in the floor and attacked Vader again, but his lightsaber cut through empty air.
The anger inside Ferus was now like liquid fuel inside him. He was feeding off Vader's rage, he was pushing every molecule of his body and feeling every molecule of the room respond to him. Everything was clear, hard-edged. His body obeyed him without any hesitation, and his mind was focused. He had no doubt that he could defeat Vader. No doubt.
And that was what the dark side brought him.
When he won, when he defeated him, he could take the victory to the Emperor, and he could be greater than Darth Vader, more powerful than even the Chosen One had been.
He charged at Vader and made contact. Vader waited a beat too long to deflect him. The blow shuddered off his body arrnor. Something inside fused and the plastoid melted. Ferus could smell buming circuits. At the same time, he detected a tremor in Vader's arm.
Suddenly he was picked up and slammed against the wall. He fought to hold onto his consciousness.
"Don't . . . get . . . cocky," Vader said.
Ferus rolled away from the blow that followed, barely escaping. He looked up. For a moment Vader was just a shape at the side of the room. For a moment, a trick of the eye or the light, he saw the room as it had been. The seats were restored, the air traffic outside flashing, the potent energy of the Force filling the room because the Jedi Masters were still alive.
Ferus felt it invade him, the sense of peace and light.
No, push it away! Listen to us! You could have been a great Jedi Knight, and they let you go! They never appreciated you!
It was true, wasn't it? Ferus saw himself as a Padawan, standing before the Masters. Taking responsibility for something that wasn't his fault. Tru's lightsaber. He had fixed it secretly. . . .
He remembered that day. He remembered the compassion in that room.
Another vision came to him, of himself as a Padawan, accepting responsibility for what he had done. The Jedi Masters sorrowful, showing him the two paths he could take. He could have stayed. He chose to go.
His choice.
The room returned to its ruined state. He was crouching, breathing hard.
Connect.
The Force was still here in the ancient stones.
The stories of all the Jedi who had lived and died here, they were here, too. His story was here. Not as distinguished as most, shorter than many, but his. He had followed the path for as long as he could, as well as he could, and the Masters had never asked for more than that.
He felt the wisdom of the Masters inside him, and he gripped that feeling with his hands and let it fill his heart. He rose. He had no doubt that they had reached out and touched him. Many hands on his shoulder, showing him. Here is one way. Here is another. Choose.
He had come so close.
He walked out of the dark side and into the light.
I am a Jedi.
Now he knew with absolute certainty that he had to be rid of the Sith Holocron. It had been slowly poisoning him. He had been a fool to think he could take what he wanted and not be corrupted. He had fallen into the Emperor's trap. Almost.
He Force-leaped over Vader, surprising him, and let himself fall into the hole in the floor. He heard Vader's chuckle.
"Run like the coward you are!"
The wind whistled past his ears as he fell. He landed safely in the Map Room. He headed for the stairs.
He took each turning at top speed, Force-leaping most of the way. He knew where to go. The heart of the building, the power core. No longer operational, it would still contain enough residual energy, if not to destroy the Sith Holocron, then to damage it. He ran through the hallways and found the central conduit that ran, he knew, straight down to the power core. He reached into his tunic.
You are throwing away your only chance at success.
This is not the kind of success I want.
The voices of darkness were a clamor inside him as he held the Sith Holocron. He threw it in. He felt something rip inside him. It was an agonizing pain that sent him down on his knees. He breathed through it, calling on the Force to help him.
He felt it lift. He was exhausted, but he was free. He was himself again.
Vader came out of nowhere, raising a gloved hand. Ferus felt himself lifted up, over Vader's head. He couldn't breathe.
"You should know before you die that your dream is dead," Vader said. "Don't you know I can bow anyone to my will?"
Ferus was slammed against the wall. He felt himself losing consciousness.
He was glad, in the end, that he would die here at the Temple. With the ghosts of his friends, his mentors, his fellow Jedi. He would become one with the Force in the place he first discovered and nourished it.
Dooku’s use of Dun Moch is evident in all of his fights--he taunts Kenobi as he toys with him in AOTC, taunts Anakin in AOTC, taunts Yoda in AOTC, taunts Windu as they fight, taunts Yoda in YDR, taunts Anakin in ROTS, etc. Vader’s form “lacks the polish of lifelong masters”--it’s sloppy in comparison. Dooku’s ability to contend and often overpower Anakin in bladelock as well as stalemate Yoda in bladelock two examples of how he can contend (if not overpower) Vader in a contest of aug. Dooku’s greater mobility and skill with telekinesis and lightning will allow him to exploit great openings in Vader’s enraged state.
You claimed in your first post that Dooku has terrible stamina, one of the most incorrect claims you’ve made through this SS.
Dynasty of Evil wrote:Lightsaber battles were brutal in their intensity; few duels lasted more than a minute. Even for a trained Jedi, the effort of all-out combat was exhausting: particularly when using the acrobatic maneuvers of Ataru.
Zannah claims that most duels end before a minute, and that “few duels lasted more”. “All-out combat was exhausting”, and Dooku engages in all-out combat with extremely powerful foes quite often. If you count the fight beginning as of the lightning exchange, Dooku fights Yoda (while exhausted) for a total of 80 seconds, whereas if you count the fight as only saber combat, it’s a 40 second long fight. Considering Dooku’s already tired and he’s capable of tiring Yoda in either an extremely long fight or an above average fight, I doubt this can be used to claim Dooku has bad stamina. Dooku duels Anakin and Obi-Wan together for a period of 40 seconds and then holds up against Zonakin for roughly the same amount of time. He duels two opponents that are extremely powerful individually, but together are a nigh-unstoppable duo for above average periods of time, then duels a Yoda+ opponent on his own for an above-average period of time. There’s no evidence for Dooku’s stamina really being that bad when he can contend with a duo of a character far inferior and reasonably superior, as well as an individual character marginally superior for above-average portions of time, leaving them exhausted as well.
Conclusion
Every point I’ve made still stands here. Dooku is far more powerful that ROTS Kenobi, who’s superior to his ANH iteration, who’s >= ESB Luke. Vader has power on par with likely his AOTC iteration, somebody that Dooku is far more powerful than. Dooku’s lightning is at a similar range of power to that of Galen Marek, evident from Dooku’s capability of pressing Yoda with it. Vader’s weakness to Dun Moch in a fight is something that will haunt him against Dooku, and Dooku’s stamina is top-notch. None of your points stand really, however. ESB Luke (by extension Vader) are not superior to ROTS Kenobi in any way, shape, or form. Dooku is far above ROTS Kenobi, and Dooku’s advantages are far greater than the limited advantages Vader possesses.
@ISV: Your turn
@EmperorCaedus @Cheth @BoD @”lorenzo.r.2nd” @Latham2000 @Syndiciate @MasterCilghal
(Tagged basically everybody who posted on thread).
 BreakofDawnLevel Seven
BreakofDawnLevel Seven
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 8:44 am
Excellent post.
 Nute_ChethrayModerator
Nute_ChethrayModerator
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 9:39 am
Finally read ISV's reply as well as IG's latest. Good work both of you
 lorenzo.r.2ndLevel Three
lorenzo.r.2ndLevel Three
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 12:48 pm
Good post. Don't like seeing that gillard system,but good nonetheless
 The lord of hungerLevel Two
The lord of hungerLevel Two
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 1st 2020, 1:31 pm

 The Fallen WarriorLevel Four
The Fallen WarriorLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:00 pm
=
The Mighty Count of Serreno!
Section I - IG’s Evidence (or Lack Thereof)
So then what is the problem? I agree that the boost is not representative of his average growth, it was the fact that he went from not being able to walk to outright stomping 5 Jedi and dueling even with a Council master in a very short period of time that impressed me. Like, the boost was just the icing on the cake powerwise, I feel you misinterpreted what I meant.
What? Why wouldn’t going from being unable to walk to being a council master tier in a short span of time be indicative of the kind of growth and improvements he would achieve without those hindrances? I provide more evidence with the Sa Cuis example that the growth continued and again as we see in your next statement…
The best you can do to counter my argument is once again appeal to the argument of incredulity. I will remind you that saying my idea is crazy, without countering it with evidence is fallacious. You do attempt to provide a measure of evidence by citing the example of Yoda not being able to lift 5 Muntuur stones and only lifting 4 by the time of TPM. Yet, as you referenced in your previous post, conflict makes force users grow, and Yoda is more powerful by quite a margin by Revenge of the Sith judging by his encounters with Dooku and SIdious respectively (more on this later). So what you are saying is stagnation kills growth, but Vader is certainly not stagnant during this time. Vader is personally responsible for the training of the Darkside Adepts of the Empire, this includes the inquisitorious who as noted by Antennis Tremayne and seen in the Hyperspace Web Strip Evasive Action Vader hand trains. Vader has his apprentice Galen Marek to train so that he can overthrow the Emperor at this time. Vader has systems to put down and keep in service of the empire and organizations to quell into submission a matter he personally attends to:
Lastly, as you know Vader also takes a personal interest in hunting Jedi survivors of Order 66. In comparison, Dooku engages in very few lightsaber duels throughout his 3 year war, Dooku spends most of his time in politics and away from the battlefield yet has a massive growth enough to compensate for the nexus of Korriban? You calling my argument “crazy” has a whole new level of irony doesn’t it? Yet I would like to run with your logic for a minute. It’s clear that Tyranus’s training of his little cadre of adepts and few lightsaber duels affords him a gargantuan amount of power growth, so then we must also concede that Vader’s training of the inquisitors, Galen Marek, and numerous battlefield and dueling scenarios affords him the same type of growth. In other words: even if we go by IG logic your arguments only serve to validate mine.
Again you misinterpreted what I was saying. I wasn’t implying you compared the two, I was saying you used two prodigies to try and explain away inconsistencies in growth, which doesn’t work at all. The entire example in itself is easily summarized by your own argument too. Anakin in the temple training with everyone else his skills are being somewhat dormant and thus he doesn’t grow that much in the interim, yet during wartime he blossoms into someone far more powerful. The same would go for Kenobi. So there is your explanation for why they are “inconsistent” in growth. They are constantly fighting and grow more as a result of that. This is your argument for Dooku too… if war increases the speed of growth then you have inadvertently poisoned this comparison above with hypocrisy. As for Sidious, he is yet another prodigy so it’s improbable to use him as a benchmark comparison to Vader, but even in this case he’s been draining the lifeforce of Byss and studying dark lore for years, on-top of having a newer and younger body to better sustain that power. He too has an explanation, it appears you merely have to read the source material to find it.
We’ll get to that later.
A greater prodigy you say? Please substantiate that. Anyway, I’m glad you brought up this comparison of training because it is indeed interesting. Luke doesn’t have the formal training, no. Luke is training on a backwater world with snakes and beasts of all sizes, but Luke is also being hand trained by Yoda. Anakin is sitting in a temple, occasionally going on field missions and sparring, but he has yet to face real conflict and he’s clearly not being trained in a very harsh environment by a very harsh teacher. Contrast that to Yoda who is “pushing Luke to his limits” everyday and you should be able to see why someone with Luke’s situation might be more combatively viable than Anakin.
He does?
George seems to imply that he has the same potential as what Anakin would have become. No, Dooku’s dismantling of Skywalker in no way translates to superiority to Luke.
Are you serious? The quote you posted just says that he wasn’t trained like a PT jedi, he wasn’t, he was trained out in the wilderness by Yoda. The quote does imply some contextual relevance to Luke’s skill, but I never argued that Luke had more sophisticated technical skill, only that he was better combatively. Also, this quote says Lucas “kept improving the sword fighting” so are you conceding that ESB Luke is a better duelist than Ben too?
Woah, what do you mean by throwing the fight? Are you saying he wasn’t giving his all? The DK quote merely says Kenobi let Vader win, but it doesn’t say he didn’t try to fight. You can clearly see in the film and every other source where Kenobi “gives up” which is when he raises his lightsaber and allows Vader to strike him down.
That doesn’t answer my question at all. Chee is responding to something in 2019, unless he explicitly said it goes for Legends he is referring to Canon. You really need to prove this refers to legends or it can actually be thrown out. Either way, I am beginning to fear you never read my first post, because all these arguments about Vader being equal to Ben during the fight actually mean nothing considering I posted three quotes and a passage saying after Vader killed Ben he got a type of boost and became better in all areas. This entire debate on Ben Kenobi has been pointless, but I’ll humor you:
Okay, even if you want to argue the quote was legends (no proof it is) you still have to get past my three aforementioned quotes. Because at the end of the day, Vader being equal or inferior to Kenobi is only a problem if we were debating ANH Vader, yet I have provided plenty of evidence suggesting Vader improved to be vastly beyond what Ben Kenobi and his previous self had shown.
Is that a sly roundabout way of saying you concede all previous points about the definition of “sport?”
I must wonder now, do you even read my posts?

It is Luke’s power “in the ways of the force” that makes him “at last” a worthy opponent to ESB Vader.
On-top of that, the Shadows of the Empire quote says he’s the most powerful. I understand that you don’t buy that because of Yoda and other powerful figures Anakin has met, but he also says it is going to be “the duel of a lifetime” and compares it’s difficulty in contrast to how easily he is dealing with fighters. In fact, the entire statement’s context is Vader musing to himself in his tie fighter about how easy everything in life is and how Luke is the only challenge he has now, how Luke is his greatest challenge ever and he looks forward to meeting a worthy opponent in battle again. So yes, Luke is Vader’s greatest challenger, there is no disputing that.
Yoda is hindered in that fight.
He’s not, I never said or implied he was. For some bold reason you have decided to say that Sidious and Yoda are incapable of ragdolling Obi-wan and Dooku and that I challenge you: prove it.
Not at all what I said, you just shoved a whole paragraph of fabricated sentences in my mouth but okay. Either or, you appeal once more to that argument of incredulity which leads me to conclude you are incapable of countering my arguments without merely chastising them for their supposed “absurdity.”
Ah, my mistake. I assumed since we were talking about the original trilogy you referenced that Yoda. Alright, if you want to dismiss the quote on the grounds it’s referring to potential that’s fine, Luke is potentially greater than all those people so that makes sense. Still doesn’t counter the two others that say he’s Vader’s best challenger though.
Did you read it?
Yes it says he’s slower than the “duelist he once was” which refers to his state at the end of Revenge of the Sith, this doesn’t at all place him below IH Kenobi or any Kenobi before his realization.
Really? So you think that Ben having an older vessel that prevents him from dueling the way he used to means he diminished in his actual power or the power he can apply in combat?
According to Vader, Kenobi’s power’s haven’t diminished at all, so the quote saying he’s slower is only saying that his applicable skill in a duel is inferior to what he could once do, not that he has lost any of his actual power. This entire argument that because Ben is about 20 years older he somehow lost his power is bogus. In the words of Han:

Section II - dOoKu rAGdOllS (An Incredibly Ironic Statement Considering IG Was Just Bitching About Ragdoll Gaps Being Absurd)
Slow down, I just explained this to you. Kenobi rushed Dooku full defenses not erected thinking his back was turned, in that second, Dooku turned around and picked him up and he couldn’t gather his energies in time due to the suddenness of the attack catching him off-guard. What part of that argument do you not understand? Kenobi’s defensive style is irrelevant if he’s not employing it at the time…

That quote doesn’t mean you think it does. Vader has cybernetic limbs and big feet, according to Galen Marek he has “an occasional clumsiness”:
Yet he’s also “sure on his feet.” This makes sense within the context of the character as the suit itself is bulky and heavy, but his “lack of polish” just means his style isn’t as pretty as Dooku’s. Vader can compensate for this in bursts as shown here:
Ferus Olin (who has been around the council masters) directly compares his skill to that of the Council Masters. The only way to reconcile that quote with this one is that it must refer to the clumsiness Vader occasionally sports which doesn’t really factor in since he can perform council level swordsmanship if he needs to anyway.
No, you just didn’t read the quote that went with my argument. I merely cited that Luke was faster than Ben and more viable, I did not argue his speed denoted greater power. Even if I were to argue that, you are making another false comparison, there is a colossal difference between being caught off guard by a burst of speed and being consistently faster than another character. Perhaps stop accusing me of double standards and start comprehending my arguments?
What? It changes everything if the opponent is caught off-guard, they can’t adequately defend themselves. Are you honestly the guy that thinks a sucker punch denotes greater speed? Because that’s the logic you are arguing.
Why is Anakin at all relevant in this scenario? Dooku has just in-capped Anakin with a kick and Dooku turned at the last minute to seize Kenobi. Anakin is not at all relevant to Kenobi being caught off-guard or this entire situation.
Because Dooku is literally making them trip over each other…
Good for Dooku that he can very methodically deal with two opponents at once, forcing them in each other’s way while deftly moving out of attack vectors and keeping them on their toes. That doesn’t translate to him being a ragdoll gap ahead of Kenobi.
Considering Dooku has an in-depth knowledge of all lightsaber forms and has a chance to regain his composure and rethink the situation, I don’t think you can actually argue that his surprise affects his combative viability at all. That’s speculation without evidence anyway.
Again, it’s just a case of you assuming things. How powerful was Mace during this period? We really don’t know, we do know that by ROTS he’s a hair away from a 9 compared to Dooku’s 8. So there’s a fair gap between the two.
Not prime or unhindered Yoda.
You mean you are actually gonna provide evidence for one of your offhanded claims?
Dialogue is important.

Yoda notes that Dooku is weaker than his Jedi self. This implies Dooku is concealing his power to decieve Yoda. Then:

When Yoda leaps overextending himself, Dooku decided to fire a torrent of lightning at Yoda’s back which sends him flying. Also as you said, this battle takes place in 20 bby which is a good distance away from ROTS meaning it has no relevance really. Revenge of the Sith Yoda is a 9, Dooku is an 8. The gap is “enormous.” Any fights prior can’t make it any smaller.
If you want to argue Dooku’s style is potentially what allows him to play with the titans that’s fine. Yoda is a midget using a highly exhaustive form that requires him to cannonball across the room to strike, Dooku is a 6’5 tall man who uses a form designed to conserve energy and keep foes at arms length. So yeah, Dooku the giant can keep the midget away for a little while and still loses every time. This will certainly help him against Vader won’t it?
This is ANH Vader, pre Ben death boost and Kuro certainly is not fodder she’s “one of the greatest Jedi”, her students are “the best in the temple” and she has the ability to phase through matter. She’s also not post prime, no idea where you got that, all the Jedi who survived Order 66 have been “honing their skills”

but even then this isn’t at all a low showing, let’s break the fight down page by page:

So Kuro uses a two-handed grip to block a one-handed strike from Vader that immediately drives her to her knees:

She leaps away and they talk a bit. She mocks him and leaps at Vader.

She tries to do a Yoda and cannonball herself at him but bounces off his block. He decides to start throwing rocks.
You cut out the next part of the fight too, here it is:

She uses her unique Chlorokinesis ability to snake some vines up Vader’s legs tying him down.

She also leaps at Vader in this state and fails to accomplish anything, he actually overpowers her:

Now she is retreating against his strength:

She uses her unique phase ability to get out of a bladelock with Vader and then disarms him:

Only for him to disarm her in turn physically overpowering her with ease:

She retreated from Vader the entire fight and everytime she directly faces him she either runs away or uses some hack of hers to distract him. These are not nigh equals and again, this is pre prime pre ESB pre ANH boost Vader. This means nothing.
You failed to actually make a compelling argument so you resort to holistic portrayal. Even this argument you fail, as Vader has shown no such incompetence as of his prime or even in the example you cited.
Vader won’t be thinking “oh he’s distracted, I’ll take him from behind!.”
Cool. Again i’m positive you haven’t read my opener because I distinctly remember putting something in there about a “Margin for Error.” Even without that, you haven’t established a good basis for why Dooku is superior to Luke anyway. All you have done is spew the same broken record over and over again about how Kenobi is the master of Soresu and Dooku is too fast for him to react to. There’s no substance, there’s no counter. It’s all just bravado.
Again that means nothing. The duel takes place before the Outer rim sieges which last five months. That means this is at LEAST five months for Kenobi to grow and become relativistic to Dooku.
Yes, because obviously holding someone at bay with one-hand denotes greater power and has nothing to do with leverage and positioning at all.
They are using their secondary forms Ataru and Shien respectively, there is a noticeable improvement against Tyranus when the duo switches forms.
Again though, Dooku being able to fight two opponents at once doesn’t denote his superiority to Kenobi. The entire claim of him being able to “effortlessly deflect” a few blows somehow translating to superiority is baseless as well.
This almost seems blatantly deceptive.
The passage is referring to Dooku kicking Kenobi. If you want to draw ragdoll tier gaps off of kicking someone that doesn’t work. Darth Maul can kick Darth Sidious back at the apex of their duel. Even if you argue that gap is smaller, Sidious is still more powerful meaning that kicks during duels mean absolutely nothing.
What? Are you arguing that force pushing your opponent denotes a vast amount of superior power? Let me point you to Dooku then:

Throughout this entire debate you have repeatedly cited Dooku’s relativity to Anakin and Kenobi at the same time, insinuating you do not think Anakin is a ragdoll tier gap above Dooku. Yet we see Anakin push Dooku, which by your logic denotes a vast gap between the two. So Anakin as of the Invisible hand is more powerful than Count Dooku. Kenobi then grows to become the equal of MFV by the end of the film who is far more powerful than IH Anakin as he has “just taken force LSD” and “jumped to a nine.” Tell me how does Dooku make up for that gap?
You are right there is no “ragdoll sequence” in the book. In the novelization, Dooku kicks Kenobi once and pushes Kenobi once, neither of which denote the superiority of the “ragdoll tier gap” between the two you keep arguing. Like it baffles me that you cite the “disproportionate strength of a barrier” and still consider it completely reasonable to argue that Kenobi is but a flick of the wrist away from Dooku. It’s not just baffling, it’s hypocritical.
Once again “the attack had been too sudden” and he thought Dooku was preoccupied with Anakin, this burst of speed means nothing.
Ah, so your double standards are on full display. Alright. So Krayt was "completely taken by surprise" and this differs from Kenobi how?


Cade has to call the lightsaber to him and leap behind Krayt all while saying “I know who I am… I am a Jedi”
Compare that to Obi-wan not even being able to muster his energies because of how sudden the attack was. So yes, the burst of speed denotes that Dooku can ragdoll an off-guard Kenobi nothing more. I’m getting tired of debunking the same arguments over and over.
You use Mace now but later in this very post you will argue that the duel was so brief that Mace “couldn’t get a feel” for Dooku’s strength. These double standards are just non-stop aren’t they? Anyway, the combat with Yoda means nothing unless you can disprove Kenobi’s relativity to Dooku. The argument I use in itself is evidence. The form changing is speculation and really nothing suggests that it hindered him combatively.
Now I’m more than confused, I have no idea what you are trying to do. Kenobi’s passive barrier is much weaker than his active barrier and passive barriers really mean nothing. Kenobi was caught off-guard, you used some random quote about Kenobi’s reactionary times being instantaneous to try to disprove something the junior novel makes painfully evident.
THE ATTACK HAD BEEN TOO SUDDEN!
Why are you arguing this? Dooku’s attack was too sudden for a Kenobi who thought that Dooku was preoccupied with Anakin, but he was wrong. Quit arguing that Kenobi’s tactical error somehow translates to a vast disparity in power, it makes you look bad.
I’ll just take a page from your book. Let’s say that Kenobi isn’t a nine, but can compete with one like MFV, that still puts him as better than Dooku, since Dooku is locked beneath IH Anakin. Again, you ignored my point about Kenobi “letting go” which gave him access to far more power.
There is a fundamental difference between augmentation and raw force power, especially in a vessel as old as Obi-wan. Also, being a shadow of Mustafar Kenobi that can contend with Anakin is not at all bad. Consider the kind of growth Kenobi must gain throughout Revenge of the Sith and juxtapose that with the unquantifiable deterioration he experienced. Now, try and prove that Ben who is compared to his prime self is beneath the Kenobi who was making Dooku sweat on the Hand.
Again, you cannot have read my first post and written this. I addressed “your powers are weak old man” as Vader’s drain, he says this to Kenobi after he overpowers him. They stand for minutes just staring at one another and Kenobi begins to sweat, then Vader says that line: “your powers are weak old man”
You aren’t reading my quotes at all, that’s all but confirmed now.


“Because luke does not believe it is possible, he fails to raise the ship.”
That statement attributes Luke’s lack of confidence as the reason he can’t lift the ship, it’s asinine that you would argue this point considering, as you said earlier; Luke can tag Vader and is out of his ragdoll range. If you truly think that Luke shares some relativity with ESB Vader then you must admit that he is above ANH Vader via his comparison with Ben, who is at least more powerful than Dark Times Vader who is capable of exceeding the X-wing feat only a few months after Revenge of the Sith:

Even if you are right about Vader’s growth and he only grew one ragdoll gap from 19-18bby that still means ANH Vader ragdolls this Vader and ANH Vader and ESB Vader have a large gap that Luke has to not be in ragdoll range from. In layman's terms (since it might be easier if I dumb this down for you) arguing Vader struggles with someone who can’t lift a small ship is fallacious and against the actual lore provided.
No your “comparison” was a gross misinterpretation of the lore for the sake of lowballing. I gave you two quotes attributing his failure to lift the X-wing to his belief in his own abilities and you tried to handwave them away by citing his response; “it’s impossible”...
No shit he thinks it’s impossible, that is why he can’t lift the damn thing in the first place.
Good on you for entirely conceding your point about the weakness of Korriban’s nexus relative to the EmpalSuRecon though. I’m impressed you can suppress your ego enough to admit you are wrong.
So you agree he’s still not tested and doesn’t give it his all right? I don’t care how much he was or was not holding back, we know he was toying:
Since we do agree he is toying and Kenobi and fact files supports this idea, it’s easy to say that him not being tested and engaging in two short lightsaber duels and getting tired is indicative of his poor stamina. The flashes of brilliance clearly don’t press him, because he is not “tested” as you so adequately described.

You implied that you had definitive proof that Dooku can exhaust Dooku due to his skill. Yoda “lacks the stamina of youth” and literally has arthritis and needs a cane to walk. In order to duel he uses the most physically exhausting form bar Juyo so of course after he deactivates his force reserves he will feel fatigue. This means nothing.

You straight up ignored my entire argument. Like, I can only assume this is willful ignorance because I can’t fathom this level of stupidity. The feats of strength Vader can perform as a cyborg are far greater than that of Anakin. This is literally compared to having very little access to the temples records, to having all of it at his fingertips from across the galaxy, which denotes it’s a huge gap. His augmentation and powerlevel means jack shit when he himself says that the feats he can perform now are better.
You argue this now, yet argued earlier his contention with mace was a showing placing him above the likes of Kenobi. To quote you: “Your double standards astound me.”
You haven’t drawn any connection between Vader being physically inferior to Yoda or why.
You haven’t backed anything up yet and Vader can still be stronger than AOTC Anakin by your quote, why must you chastise me for arguing something you have yet to even address?
The Mighty Count of Serreno!
Section I - IG’s Evidence (or Lack Thereof)
IG wrote:No, my argument does not hinge on the idea that Vader’s growth was predicated around that single boost. The boost is not representative of his average annual growth. If somebody gains a massive power boost, we can’t apply that to their normal growth. We see Jacen Solo in Legacy of the Force: Sacrifice gains a massive sacrificial power boost from killing Mara Jade. He doesn’t gain these massive power boosts every day, not every week, nor every month. Likewise Anakin gains a massive power boost by jumping to the DS. Yet he isn’t going to be gaining boosts akin to that every other day or so, had he survived.
So then what is the problem? I agree that the boost is not representative of his average growth, it was the fact that he went from not being able to walk to outright stomping 5 Jedi and dueling even with a Council master in a very short period of time that impressed me. Like, the boost was just the icing on the cake powerwise, I feel you misinterpreted what I meant.
IG wrote:
Likewise, Vader’s killing of Roan Shryne “firm[ed]” Vader’s faith in “the power of the dark side”. You haven’t provided evidence for why Vader going from, as you’ve said “a walking pile of burn garbage” to one whose “true apprenticeship could begin” is representative of normal growth. It’s evidently indicative of a massive boost in power.
What? Why wouldn’t going from being unable to walk to being a council master tier in a short span of time be indicative of the kind of growth and improvements he would achieve without those hindrances? I provide more evidence with the Sa Cuis example that the growth continued and again as we see in your next statement…
IG wrote:it doesn’t require a citation, as I’m appealing to common sense. We see masters as they grow closer and closer to achieving their potential stagnating. Yoda says that he used to be able to lift 5 Muntuur stones, now (around pre-TPM iirc) he’s only able to lift 4. Vader hasn’t achieved nearly as much of his (revamped) suited potential in 19 BBY as he has in 10 BBY, so logically he’ll grow more when he has more of his potential to achieve than less, evident by my Padawan analogy.
The best you can do to counter my argument is once again appeal to the argument of incredulity. I will remind you that saying my idea is crazy, without countering it with evidence is fallacious. You do attempt to provide a measure of evidence by citing the example of Yoda not being able to lift 5 Muntuur stones and only lifting 4 by the time of TPM. Yet, as you referenced in your previous post, conflict makes force users grow, and Yoda is more powerful by quite a margin by Revenge of the Sith judging by his encounters with Dooku and SIdious respectively (more on this later). So what you are saying is stagnation kills growth, but Vader is certainly not stagnant during this time. Vader is personally responsible for the training of the Darkside Adepts of the Empire, this includes the inquisitorious who as noted by Antennis Tremayne and seen in the Hyperspace Web Strip Evasive Action Vader hand trains. Vader has his apprentice Galen Marek to train so that he can overthrow the Emperor at this time. Vader has systems to put down and keep in service of the empire and organizations to quell into submission a matter he personally attends to:
Hero's Guide wrote:Aiding the Emperor in his monumental responsibilities is his apprentice and confidant, the formidable Lord Vader-a tragic hero who serves as the Emperor's strength when diplomacy fails. Vader personally battles against the Empire's most dangerous enemies-those individuals and organizations too powerful or too well-defended for the Imperial military alone to overcome. And as a price for his noble efforts, Lord Vader must suffer eternal confinement within his life-sustaining armor, without which he would surely perish within moments.
Lastly, as you know Vader also takes a personal interest in hunting Jedi survivors of Order 66. In comparison, Dooku engages in very few lightsaber duels throughout his 3 year war, Dooku spends most of his time in politics and away from the battlefield yet has a massive growth enough to compensate for the nexus of Korriban? You calling my argument “crazy” has a whole new level of irony doesn’t it? Yet I would like to run with your logic for a minute. It’s clear that Tyranus’s training of his little cadre of adepts and few lightsaber duels affords him a gargantuan amount of power growth, so then we must also concede that Vader’s training of the inquisitors, Galen Marek, and numerous battlefield and dueling scenarios affords him the same type of growth. In other words: even if we go by IG logic your arguments only serve to validate mine.
IG wrote:
Except I wasn’t comparing Anakin to Obi-Wan at all. I literally pointed out two periods of their lives and compared the growth there to another period in their lives. I compared Anakin’s TPM-AOTC Growth to his AOTC-ROTS growth and stated that he grew more during the latter period than the former. I likewise compared Kenobi’s growth in the two time periods. Given that both of the characters’ growth is not linear, it’s logical to proclaim that all growth isn’t linear. Other examples of growths that aren’t linear is Sidious’ from TPM to ROTS compared to ROTJ to DE, therefore showing that there’s no validity in claiming linear growth.
Again you misinterpreted what I was saying. I wasn’t implying you compared the two, I was saying you used two prodigies to try and explain away inconsistencies in growth, which doesn’t work at all. The entire example in itself is easily summarized by your own argument too. Anakin in the temple training with everyone else his skills are being somewhat dormant and thus he doesn’t grow that much in the interim, yet during wartime he blossoms into someone far more powerful. The same would go for Kenobi. So there is your explanation for why they are “inconsistent” in growth. They are constantly fighting and grow more as a result of that. This is your argument for Dooku too… if war increases the speed of growth then you have inadvertently poisoned this comparison above with hypocrisy. As for Sidious, he is yet another prodigy so it’s improbable to use him as a benchmark comparison to Vader, but even in this case he’s been draining the lifeforce of Byss and studying dark lore for years, on-top of having a newer and younger body to better sustain that power. He too has an explanation, it appears you merely have to read the source material to find it.
IG wrote: My statements of incredulity were in regards to the fact that Vader’s growth being linear is completely unfounded and that Luke’s 19 ragdoll gap superiority to Shryne, to be quite frank, is utter bull. Tell me ISV, if Vader grows a ragdoll gap a year, why does he struggle with Ben Kenobi?
We’ll get to that later.
IG wrote: Consider that under your premise of Vader >> ESB Luke > Ben ~ ROTS Kenobi ~ Dooku that you fail to account for AOTC Anakin. Anakin is a greater prodigy with 10 years of formal training, as a sharp contrast to Luke being a lesser prodigy with only 7 months (as you’ve cited later on in your post) of informal training.
A greater prodigy you say? Please substantiate that. Anyway, I’m glad you brought up this comparison of training because it is indeed interesting. Luke doesn’t have the formal training, no. Luke is training on a backwater world with snakes and beasts of all sizes, but Luke is also being hand trained by Yoda. Anakin is sitting in a temple, occasionally going on field missions and sparring, but he has yet to face real conflict and he’s clearly not being trained in a very harsh environment by a very harsh teacher. Contrast that to Yoda who is “pushing Luke to his limits” everyday and you should be able to see why someone with Luke’s situation might be more combatively viable than Anakin.
IG wrote:
Logically then, given Anakin has a greater potential than Luke, he is more powerful than Luke. Dooku dismisses Anakin during one of his “flashes of brilliance”, times when Anakin performs at a far, far better state than his normal one. Thus making it evident of Dooku’s (vast) superiority to ESB Luke.
He does?
Rolling Stones #375 wrote:"He tries it with anybody he thinks might be more powerful, which is what the Emperor was looking for in the first place: somebody who would be more powerful than he was and could help him rule the universe. But Obi-Wan screwed that up by cutting of his arms and legs and burning him up. From then on, he wasn't as strong as the Emperor -- he was like Darth Maul or Count Dooku. He wasn't what he was supposed to become. But the son could become that."
George seems to imply that he has the same potential as what Anakin would have become. No, Dooku’s dismantling of Skywalker in no way translates to superiority to Luke.
IG wrote:Lucas also indicates that Luke’s training is subpar comparative to a normal Jedi in the following quote:
Star Wars Featurette: The Birth of the Lightsaber wrote:
“In every episode from 4, 5, and 6, I kept improving the sword fighting because the assumption was that Luke was getting to be a better fighter, he was learning more, but at the same time he still wasn’t being trained as an original Jedi would have been trained.”
Are you serious? The quote you posted just says that he wasn’t trained like a PT jedi, he wasn’t, he was trained out in the wilderness by Yoda. The quote does imply some contextual relevance to Luke’s skill, but I never argued that Luke had more sophisticated technical skill, only that he was better combatively. Also, this quote says Lucas “kept improving the sword fighting” so are you conceding that ESB Luke is a better duelist than Ben too?
IG wrote:None of them actually make it clear that Ben gave up. I’ve always been of the opinion that he’s thrown the fight, something that the DK book quote makes evident
Woah, what do you mean by throwing the fight? Are you saying he wasn’t giving his all? The DK quote merely says Kenobi let Vader win, but it doesn’t say he didn’t try to fight. You can clearly see in the film and every other source where Kenobi “gives up” which is when he raises his lightsaber and allows Vader to strike him down.
IG wrote:As for your point on Chee, the tweet is in response to a question about the 6, 4, 2 quote. Meaning that this is supporting evidence that the 6, 4, 2 argument stands. Chee follows Lucas’ lead on this, and declares that Obi Wan is indeed stronger than Vader, but power levels (raw power a force wielder can use) aren’t the only factor in a fight.
That doesn’t answer my question at all. Chee is responding to something in 2019, unless he explicitly said it goes for Legends he is referring to Canon. You really need to prove this refers to legends or it can actually be thrown out. Either way, I am beginning to fear you never read my first post, because all these arguments about Vader being equal to Ben during the fight actually mean nothing considering I posted three quotes and a passage saying after Vader killed Ben he got a type of boost and became better in all areas. This entire debate on Ben Kenobi has been pointless, but I’ll humor you:
IG wrote:
As for your arguments on the quote’s validity, the first two revolve around the core idea that the terminology “maybe” and “probably” are ambiguous, and that it makes no sense to declare that Ben > Vader solely on these quotes. Yet the general idea is that Chee’s quote allows reconciliation of the idea Ben > Vader. We see how his tweet was in response to a question about the quote, where he goes along with Lucas’ intent and declares Ben > Vader in raw power is canonically fact.
Okay, even if you want to argue the quote was legends (no proof it is) you still have to get past my three aforementioned quotes. Because at the end of the day, Vader being equal or inferior to Kenobi is only a problem if we were debating ANH Vader, yet I have provided plenty of evidence suggesting Vader improved to be vastly beyond what Ben Kenobi and his previous self had shown.
IG wrote:Which is all fair,
Is that a sly roundabout way of saying you concede all previous points about the definition of “sport?”
IG wrote:but being a better combatant than somebody isn’t being more powerful than them. Ben’s an old man, so while his raw power is still at the level of Vader, his combatative skill is, to be quite frank, shit. To contrast, Luke lacks the raw power that Obi-Wan has, but he’s young, so naturally he’s more mobile than a man nearing the age of 60.
I must wonder now, do you even read my posts?
It is Luke’s power “in the ways of the force” that makes him “at last” a worthy opponent to ESB Vader.
On-top of that, the Shadows of the Empire quote says he’s the most powerful. I understand that you don’t buy that because of Yoda and other powerful figures Anakin has met, but he also says it is going to be “the duel of a lifetime” and compares it’s difficulty in contrast to how easily he is dealing with fighters. In fact, the entire statement’s context is Vader musing to himself in his tie fighter about how easy everything in life is and how Luke is the only challenge he has now, how Luke is his greatest challenge ever and he looks forward to meeting a worthy opponent in battle again. So yes, Luke is Vader’s greatest challenger, there is no disputing that.
IG wrote:Here however, you try to claim that Luke’s mobility and greater speed are evidence of why he’s faster and more powerful than Ben. The double standards here astound me. You yourself claim that Luke’s greater speed than Ben shows superiority, but when I cite Dooku moving so fast that Kenobi is incapable of throwing up a defense to block his attacks, you claim that it’s an incorrect comparison? Here, I actually have to point out a glaring flaw with your entire logic, namely Vader’s linear ragdoll gap growth. According to you, Vader grows a ragdoll gap each year, meaning he’s jumped 3 from ANH to ESB, and Luke being outside his ragdoll range means that he’s at least a single ragdoll gap above Ben Kenobi, whom you claim is ~ ROTS Kenobi and therefore ~ Dooku. Yet not even Darth Sidious or Yoda are capable of ragdolling Dooku or Obi-Wan. In fact, Yoda is incapable of doing this to the degree that he’s forced to fight Dooku and push him back “slowly”.
Yoda is hindered in that fight.
IG wrote:Somehow Vader as of ROTJ is a ragdoll gap above the likes of Yoda and Darth Sidious?
He’s not, I never said or implied he was. For some bold reason you have decided to say that Sidious and Yoda are incapable of ragdolling Obi-wan and Dooku and that I challenge you: prove it.
IG wrote:That’s a completely insane argument, even by your standards. For one, Lucas himself explicitly states Vader in his suit could never become as powerful as Sidious was. He explicitly claims Vader can only become “80%” of Sidious. And that’s Vader’s suited potential, not his actualized power as of Return of the Jedi.
Not at all what I said, you just shoved a whole paragraph of fabricated sentences in my mouth but okay. Either or, you appeal once more to that argument of incredulity which leads me to conclude you are incapable of countering my arguments without merely chastising them for their supposed “absurdity.”
IG wrote:I was referring to ROTS Yoda. Whether Vader can or cannot defeat Yoda as of ANH (which I highly doubt, and it’s completely irrelevant anyway) is something I doubt we need to debate here. If Luke > all Jedi before that Vader’s met, that’s evidently including Windu, ROTS Kenobi, Yoda, etc, and the claim that ESB Luke > Yoda is something that’s easily refutable, namely through Lucas’ comments on it.
Ah, my mistake. I assumed since we were talking about the original trilogy you referenced that Yoda. Alright, if you want to dismiss the quote on the grounds it’s referring to potential that’s fine, Luke is potentially greater than all those people so that makes sense. Still doesn’t counter the two others that say he’s Vader’s best challenger though.
IG wrote:The quote clearly referring to Vader in his suited iteration means Luke is a greater combatant than Ben, but nothing in regards to their raw power with the force.
Did you read it?
IG wrote:Star Wars in 100 Scenes wrote:
Slowed by age, Obi-Wan is not the duelist he once was.
Meaning that Kenobi’s old age makes him a far slower duelist. One’s overall skill is a mix of raw power and technical skill, raw power affecting your augmentation and overall combat performance. Kenobi is explicitly “not the duelist he once was”, indicating a great disparity between his ROTS and ANH iterations.
Yes it says he’s slower than the “duelist he once was” which refers to his state at the end of Revenge of the Sith, this doesn’t at all place him below IH Kenobi or any Kenobi before his realization.
IG wrote:His ability in the force has diminished, as has his technical skill, leaving him a far worse combatant than usual.
Really? So you think that Ben having an older vessel that prevents him from dueling the way he used to means he diminished in his actual power or the power he can apply in combat?
A New Hope Jr. Novel wrote:Where is he? How could he vanish? What sort of trickery is this? He had assumed Obi-Wan's study of the Force had ended long ago, and that his powers had diminished over time. But Vader was wrong.
According to Vader, Kenobi’s power’s haven’t diminished at all, so the quote saying he’s slower is only saying that his applicable skill in a duel is inferior to what he could once do, not that he has lost any of his actual power. This entire argument that because Ben is about 20 years older he somehow lost his power is bogus. In the words of Han:
Section II - dOoKu rAGdOllS (An Incredibly Ironic Statement Considering IG Was Just Bitching About Ragdoll Gaps Being Absurd)
IG wrote:Obi-Wan is surprised that Dooku can hit him, yes, but that’s not refuting my argument. If Dooku is capable of taking the master of a completely defensive style off guard and then taking him out
Slow down, I just explained this to you. Kenobi rushed Dooku full defenses not erected thinking his back was turned, in that second, Dooku turned around and picked him up and he couldn’t gather his energies in time due to the suddenness of the attack catching him off-guard. What part of that argument do you not understand? Kenobi’s defensive style is irrelevant if he’s not employing it at the time…
IG wrote:Vader’s style “lacks the polish of lifelong masters”. He lacks the technical refinement that all “lifelong masters”, such as Kenobi, Windu, Dooku, Yoda, etc have.
That quote doesn’t mean you think it does. Vader has cybernetic limbs and big feet, according to Galen Marek he has “an occasional clumsiness”:
The Force Unleashed wrote:For all his size and occasional clumsiness, the Dark Lord was sure on his feet. He landed upright and launched himself back into the fray.
Yet he’s also “sure on his feet.” This makes sense within the context of the character as the suit itself is bulky and heavy, but his “lack of polish” just means his style isn’t as pretty as Dooku’s. Vader can compensate for this in bursts as shown here:
The Last of The Jedi: Secret Weapon wrote:Break it down, Ferus.
Obi-Wan? That was what he would say, in that cool way that could be so annoying.
Break down the movement; don't see it as a blur. You 're a Jedi - yes, you are! - so be a Jedi.
He didn't feel like a Jedi. But he would obey that voice and try to break it down.
He closed his eyes and grabbed the memory. This time he struggled to leave his feelings behind. He had to see it clear.
He saw Darth Vader move now. He saw the curl of his cape. The way he turned his body, the position of his feet, the way his arm moved. He had used a classic Jedi shun move, rotating the lightsaber 360 degrees, but the rotation had moved so fast he'd been unable to track it.
Break it down.
Form IV. Then Form VII, the most advanced Jedi form. Done aggressively, with impeccable control.
Coldness gripped his heart. Jedi moves.
The movement had been done with a grace and finesse that rendered it not part of a drill but part of Vader's body. He brought an individual flair to it that made it his own.
Something familiar about that form. An aggression, a confidence ... It struck a memory he couldn't touch. But who could it be?
If he could only know how old Vader was. Had he been on the Council? Such expertise suggested it.
I know him. I know the way he moves.
But everyone he'd studied with was dead. He couldn't say for certain that every Jedi he'd ever met was dead, but he knew the fate of all the Padawans. It had to have been an instructor, or perhaps a Jedi Master who had been away for long periods, so long he had lost his connection to the Jedi Temple, and Palpatine had exploited it. ...
How could a Jedi be turned? It didn't seem possible, not to any Jedi he had personally known.
Ferus Olin (who has been around the council masters) directly compares his skill to that of the Council Masters. The only way to reconcile that quote with this one is that it must refer to the clumsiness Vader occasionally sports which doesn’t really factor in since he can perform council level swordsmanship if he needs to anyway.
IG wrote:Again the double standards. Why is speed not denoting anything? Your entire argument for Ben < ESB Luke revolves around the central premise that he’s faster and more mobile than him, so he has more strength in the force through a speed comparison.
No, you just didn’t read the quote that went with my argument. I merely cited that Luke was faster than Ben and more viable, I did not argue his speed denoted greater power. Even if I were to argue that, you are making another false comparison, there is a colossal difference between being caught off guard by a burst of speed and being consistently faster than another character. Perhaps stop accusing me of double standards and start comprehending my arguments?
IG wrote:Given that this is an active combat situation, perhaps Kenobi is off-guard, yes, but that doesn’t change the fact that before he can so much as react, we see Dooku move so quickly that Kenobi cannot counter his attack.
What? It changes everything if the opponent is caught off-guard, they can’t adequately defend themselves. Are you honestly the guy that thinks a sucker punch denotes greater speed? Because that’s the logic you are arguing.
IG wrote: If you can make speed comparisons, you have to deal with them too. This is no “burst of speed in equals”, as you claim. Dooku’s capable of fighting at this level against two high level foes, Anakin and Obi-Wan at the same time.
Why is Anakin at all relevant in this scenario? Dooku has just in-capped Anakin with a kick and Dooku turned at the last minute to seize Kenobi. Anakin is not at all relevant to Kenobi being caught off-guard or this entire situation.
IG wrote:Consider that if there’s a duo and both of them stand a chance at soloing, then there’s going to be an immense stomp happening. That clearly doesn’t happen here.
Because Dooku is literally making them trip over each other…
Revenge of the Sith wrote:
How lovely for you." Dooku neatly sidestepped, cutting at the boy's leg, yet Skywalker's blade met the cut as he passed and he managed to sweep his blade behind his head to slap aside the casual thrust Dooku aimed at the back of his neck-but his clumsy charge had put him in Kenobi's path, so that the Jedi Master had to Force-roll over his partner's head.
Directly at Dooku's upraised blade.
Kenobi drove a slash at the scarlet blade while he pivoted in the air, and again Dooku sidestepped so that now it was Kenobi in Skywalker's way.
"Really," Dooku said, "this is pathetic."
Oh, they were certainly energetic enough, leaping and whirling, raining blows almost at random, cutting chairs to pieces and Force-hurling them in every conceivable direction, while Dooku continued, in his gracefully methodical way, to out-maneuver them so thoroughly it was all he could to do keep from laughing out loud.
It was a simple matter of countering their tactics, which were depressingly straightforward; Skywalker was the swift one, whooshing here and there like a spastic hawk-bat-attempting a Jedi variant of neek-in-the-middle so they could come at him from both sides-while Kenobi came on in a measured Shii-Cho cadence, deliberate as a lumberdroid, moving step by step, cutting off the angles, clumsy but relentlessly dogged as he tried to chivvy Dooku into a corner.
Whereas all Dooku need do was to slip from one side to another-and occasionally flip over a head here and there-so that he could fight each of them in turn, rather than both of them at the same time. He supposed that in their own milieu, they might actually prove reasonably effective; it was clear that their style had been developed by fighting as a team against large numbers of opponents. They were not prepared to fight together against a single Force-user, certainly not one of Dooku's power; he, on the other hand, had always fought alone. It was laughably easy to keep the Jedi tripping and stumbling and getting in each other's way.
Good for Dooku that he can very methodically deal with two opponents at once, forcing them in each other’s way while deftly moving out of attack vectors and keeping them on their toes. That doesn’t translate to him being a ragdoll gap ahead of Kenobi.
IG wrote:You cite Kenobi “stonewalling” Dooku earlier in your first post, yet Dooku’s caught utterly by surprise at Kenobi’s rapid change in form.
Considering Dooku has an in-depth knowledge of all lightsaber forms and has a chance to regain his composure and rethink the situation, I don’t think you can actually argue that his surprise affects his combative viability at all. That’s speculation without evidence anyway.
IG wrote:Just months from ROTS, Windu fights Dooku, and Windu attempts to strike Dooku down. Dooku seems to easily deflect the blow and mocks Windu to his face about it.
Again, it’s just a case of you assuming things. How powerful was Mace during this period? We really don’t know, we do know that by ROTS he’s a hair away from a 9 compared to Dooku’s 8. So there’s a fair gap between the two.
IG wrote:Likewise Dooku is able to take blows from Yoda himself on Vjun, and is only pushed back “slowly”, while taunting Yoda the entire time.
Not prime or unhindered Yoda.
IG wrote:In AOTC Dooku and Yoda fight in a relatively close fight, with an exhausted Dooku managing to exhaust Yoda (I’ll cite that in my rebuttal)
You mean you are actually gonna provide evidence for one of your offhanded claims?
IG wrote: We then see that Dooku is capable of contending and practically beating Yoda in 20 BBY in the comic Yoda Uncovered.
Dialogue is important.
Yoda notes that Dooku is weaker than his Jedi self. This implies Dooku is concealing his power to decieve Yoda. Then:
When Yoda leaps overextending himself, Dooku decided to fire a torrent of lightning at Yoda’s back which sends him flying. Also as you said, this battle takes place in 20 bby which is a good distance away from ROTS meaning it has no relevance really. Revenge of the Sith Yoda is a 9, Dooku is an 8. The gap is “enormous.” Any fights prior can’t make it any smaller.
IG wrote:We clearly see here that he contends with Yoda in bladelock, then Yoda jumps away and attempts to flip over Dooku, but Dooku blasts him away with lightning. This is an undeniable showing of nigh-parity. If Dooku, as you claim, is extremely far beneath Yoda per the tiering system, then why is he able to perform this well? Is it because perhaps Dooku is not so weak that he would be stomped by his master of by Yoda? As you claim, maybe Dooku doesn’t have raw power on par with the PT titans, or even near them (I’m not claiming this is true, to clarify). But even if this is true, Dooku’s ability to contend with foes with (as you claim) far greater raw power than him is an undeniable advantage he has.
If you want to argue Dooku’s style is potentially what allows him to play with the titans that’s fine. Yoda is a midget using a highly exhaustive form that requires him to cannonball across the room to strike, Dooku is a 6’5 tall man who uses a form designed to conserve energy and keep foes at arms length. So yeah, Dooku the giant can keep the midget away for a little while and still loses every time. This will certainly help him against Vader won’t it?
IG wrote:Vader just hasn’t shown the ability to compete with a tier 9 fighter like Yoda the way Dooku has. Dooku has been able to resist Yoda’s offensive onslaught and leave his former master exhausted for it all those times. To contrast, Vader has low showings against fodder like a post-prime An’ya Kuro
This is ANH Vader, pre Ben death boost and Kuro certainly is not fodder she’s “one of the greatest Jedi”, her students are “the best in the temple” and she has the ability to phase through matter. She’s also not post prime, no idea where you got that, all the Jedi who survived Order 66 have been “honing their skills”
but even then this isn’t at all a low showing, let’s break the fight down page by page:
So Kuro uses a two-handed grip to block a one-handed strike from Vader that immediately drives her to her knees:
She leaps away and they talk a bit. She mocks him and leaps at Vader.
She tries to do a Yoda and cannonball herself at him but bounces off his block. He decides to start throwing rocks.
You cut out the next part of the fight too, here it is:
She uses her unique Chlorokinesis ability to snake some vines up Vader’s legs tying him down.
She also leaps at Vader in this state and fails to accomplish anything, he actually overpowers her:
Now she is retreating against his strength:
She uses her unique phase ability to get out of a bladelock with Vader and then disarms him:
Only for him to disarm her in turn physically overpowering her with ease:
She retreated from Vader the entire fight and everytime she directly faces him she either runs away or uses some hack of hers to distract him. These are not nigh equals and again, this is pre prime pre ESB pre ANH boost Vader. This means nothing.
IG wrote:
Should we consider Darth Vader, a character that has unfavorable showings against fodder like Kuro to be a top tier? Should we consider Vader, somebody that’s shown time and time again his utter incompetence when dealing with powerful foes to be on par with a master such as Dooku? Should the character holistically portrayed to be with the likes of TPM Maul, or even TPM Kenobi be considered for superiority to somebody that gave Yoda the fight of his life several times and practically beat him once?
You failed to actually make a compelling argument so you resort to holistic portrayal. Even this argument you fail, as Vader has shown no such incompetence as of his prime or even in the example you cited.
IG wrote:The attack had been too sudden, yes. But this is active combat, there is a time Kenobi can be taken by surprise, but the fact that Dooku’s able to do so means that he’s able to engineer and exploit openings in others’ defenses, something that Vader will inevitably fall to.
Vader won’t be thinking “oh he’s distracted, I’ll take him from behind!.”
IG wrote:
We see in Vader’s duels with Luke during ESB and ROTJ that he is prone to utilizing long, sweeping strikes. Dooku can easily take advantage of this, the example being his fight with Kenobi in ROTS, where he’s able to easily take Kenobi out by exploiting the openings he leaves. Vader’s somebody that has been countered by a lesser prodigy than Anakin in Luke during ESB, even being injured in it.
Cool. Again i’m positive you haven’t read my opener because I distinctly remember putting something in there about a “Margin for Error.” Even without that, you haven’t established a good basis for why Dooku is superior to Luke anyway. All you have done is spew the same broken record over and over again about how Kenobi is the master of Soresu and Dooku is too fast for him to react to. There’s no substance, there’s no counter. It’s all just bravado.
IG wrote:Expanding on Dooku’s superiority to Kenobi:
https://www.youtube.com/watch?v=OcXaicGvcvA
In the link above, Dooku fights both Kenobi and Skywalker evenly (if not holding an advantage) for a period of over a minute. At approximately 1:01, we see Dooku remove Kenobi from the fight with ease for a time. Throughout we also see Dooku’s ability to fight with great mobility, something that gives him an undeniable advantage against Vader’s restricted mobility. At around 2:04, we see Dooku utilize a force blast that knocks back both Anakin and Obi-Wan, pushing them to their knees. Given the disproportionate strength of a barrier and the fact that both Kenobi and Skywalker had them up at the time, we can conclude that Dooku’s superiority to Kenobi is all but fact. Then we see Dooku overpowering Kenobi’s superior in Anakin in bladelock at 2:52.
Again that means nothing. The duel takes place before the Outer rim sieges which last five months. That means this is at LEAST five months for Kenobi to grow and become relativistic to Dooku.
IG wrote:As for Revenge of the Sith itself, we see numerous times in the fight Dooku’s evident superiority to Kenobi:
Revenge of the Sith wrote:
Anakin launched himself at Dooku’s back and the count half turned, gesturing casually while holding Obi-Wan at bay with an elegant one-handed bind.
Yes, because obviously holding someone at bay with one-hand denotes greater power and has nothing to do with leverage and positioning at all.
IG wrote:
Dooku is able to casually throw chairs at Anakin while the latter charges at Dooku, simultaneously holding Kenobi at bay one-handedly. Consider that Dooku shows seemingly no strain throughout, and is able to counter Kenobi while utilizing the force to throw stuff at Anakin.
Revenge of the Sith wrote:
While effortlessly deflecting a rain of blue-streaking cuts from Kenobi
They are using their secondary forms Ataru and Shien respectively, there is a noticeable improvement against Tyranus when the duo switches forms.
Again though, Dooku being able to fight two opponents at once doesn’t denote his superiority to Kenobi. The entire claim of him being able to “effortlessly deflect” a few blows somehow translating to superiority is baseless as well.
IG wrote:
You claim that the “whipcrack” of energy ragdoll and the ragdoll shown in the movie where Dooku kicks Anakin back and then chokes Kenobi are the same. Yet this is evidently not the case. The scene in question, where Kenobi attempts to double-team Dooku and gets caught off-guard is depicted after Dooku flings Kenobi across the room effortlessly.
Revenge of the Sith wrote:
Before the pieces could even hit the floor Dooku was in motion, landing a spinning side-stamp that folded Skywalker in half; he used his last burst of dark power [....] knocking the Jedi master back down the stairs.
This almost seems blatantly deceptive.
Revenge of the Sith wrote:Kenobi reached the top of the stairs and a single slash of his lightsaber dismantled both droids. Before their pieces could even hit the floor Dooku was in motion, landing a spinning side-stamp that folded Skywalker in half; he used his last burst of dark power to continue his spin into a blindingly fast wheel-kick that brought his heel against the point of Kenobi's chin with a crack like the report of a huge-bore slugthrower, knocking the Jedi Master back down the stairs. Sounded like he'd broken his neck.
The passage is referring to Dooku kicking Kenobi. If you want to draw ragdoll tier gaps off of kicking someone that doesn’t work. Darth Maul can kick Darth Sidious back at the apex of their duel. Even if you argue that gap is smaller, Sidious is still more powerful meaning that kicks during duels mean absolutely nothing.
IG wrote:This part specifically is where Kenobi is removed from the fight, similar to the section of the JN you cited. The part that Dooku flings Kenobi away with a “whipcrack” of power is earlier on, and is depicted in the film as Dooku pushing Obi-Wan, not choking him. There’s no evidence that Kenobi is caught by surprise when flung across the room by surprise the first time, and while it’s certainly possible that he only had a passive barrier up, Dooku still effortlessly chucks him away, and since there’s no evidence to the contrary, I can attribute this to Dooku’s own skill and power being greater than that of Kenobi’s.
What? Are you arguing that force pushing your opponent denotes a vast amount of superior power? Let me point you to Dooku then:
Throughout this entire debate you have repeatedly cited Dooku’s relativity to Anakin and Kenobi at the same time, insinuating you do not think Anakin is a ragdoll tier gap above Dooku. Yet we see Anakin push Dooku, which by your logic denotes a vast gap between the two. So Anakin as of the Invisible hand is more powerful than Count Dooku. Kenobi then grows to become the equal of MFV by the end of the film who is far more powerful than IH Anakin as he has “just taken force LSD” and “jumped to a nine.” Tell me how does Dooku make up for that gap?
IG wrote:The quote from the ROTS JN you provided states that Kenobi was caught off guard when Dooku choked him, but that’s clearly not what Stover references during the “ragdoll” sequence of his novel.
You are right there is no “ragdoll sequence” in the book. In the novelization, Dooku kicks Kenobi once and pushes Kenobi once, neither of which denote the superiority of the “ragdoll tier gap” between the two you keep arguing. Like it baffles me that you cite the “disproportionate strength of a barrier” and still consider it completely reasonable to argue that Kenobi is but a flick of the wrist away from Dooku. It’s not just baffling, it’s hypocritical.
IG wrote:Except there’s no evidence that Kenobi was caught by surprise and there’s no evidence that this was merely a quick burst of speed as opposed to Dooku having just that much better augmentative capability than Kenobi does.
Once again “the attack had been too sudden” and he thought Dooku was preoccupied with Anakin, this burst of speed means nothing.
IG wrote:You mention how barriers are easy to throw up in your Krayt comparison, but Cade isn’t using TK on Krayt then, he completely catches Krayt by surprise and takes him out with a saber attack. To contrast, Dooku augments himself sufficiently that Kenobi isn’t given the option to react in the example I’ve cited.
Ah, so your double standards are on full display. Alright. So Krayt was "completely taken by surprise" and this differs from Kenobi how?
Cade has to call the lightsaber to him and leap behind Krayt all while saying “I know who I am… I am a Jedi”
Compare that to Obi-wan not even being able to muster his energies because of how sudden the attack was. So yes, the burst of speed denotes that Dooku can ragdoll an off-guard Kenobi nothing more. I’m getting tired of debunking the same arguments over and over.
IG wrote:
1. Dooku’s ability to counter attacks from Mace Windu a few months before ROTS with ease and nearly stalemate Yoda on several occasions, combined with the fact that Dooku is caught off-guard by Kenobi and Anakin’s change in form from Shii-Cho/Ataru to Soresu and Shien to Djem So respectively shows your argument is wrong.
You use Mace now but later in this very post you will argue that the duel was so brief that Mace “couldn’t get a feel” for Dooku’s strength. These double standards are just non-stop aren’t they? Anyway, the combat with Yoda means nothing unless you can disprove Kenobi’s relativity to Dooku. The argument I use in itself is evidence. The form changing is speculation and really nothing suggests that it hindered him combatively.
IG wrote:2. While Kenobi may not have had an active barrier up, he certainly had a passive barrier up given the situation is in active combat, and as we’re speaking of two separate incidents within the fight, it’s safe to say that Kenobi wasn’t necessarily caught off-guard/by surprise.
Now I’m more than confused, I have no idea what you are trying to do. Kenobi’s passive barrier is much weaker than his active barrier and passive barriers really mean nothing. Kenobi was caught off-guard, you used some random quote about Kenobi’s reactionary times being instantaneous to try to disprove something the junior novel makes painfully evident.
IG wrote:3. Yet Kenobi wasn’t caught off-guard by Dooku’s assault, there’s no evidence saying he was. Dooku is able to augment himself so much that Kenobi is unable to defend himself and is flung across the room.
THE ATTACK HAD BEEN TOO SUDDEN!
Why are you arguing this? Dooku’s attack was too sudden for a Kenobi who thought that Dooku was preoccupied with Anakin, but he was wrong. Quit arguing that Kenobi’s tactical error somehow translates to a vast disparity in power, it makes you look bad.
IG wrote:Kenobi being able to deflect force blasts is not a showing of parity whatsoever. Kenobi’s barrier allows him to do so. In the Gillardian tiering system you cite, Kenobi is explicitly an “8”. It’s completely false to claim that Kenobi magically jumps to a 9 on Mustafar. Gillard uses “Obi Wan is an 8” as a blanket statement encompassing ROTS. Consider that Kenobi and Anakin both have intimate knowledge of each other’s forms, and while this link goes both ways, Kenobi benefits moreso from it than Anakin, as Anakin’s gone essentially batshit in this fight, and Kenobi being a defensive fighter gains more of an advantage the whole fight if he knows what his opponent’s next move will be. Considering that Kenobi also gives ground the whole fight, it’s pretty obvious that Anakin holds an upper hand… until he makes a fatal blunder.
I’ll just take a page from your book. Let’s say that Kenobi isn’t a nine, but can compete with one like MFV, that still puts him as better than Dooku, since Dooku is locked beneath IH Anakin. Again, you ignored my point about Kenobi “letting go” which gave him access to far more power.
IG wrote:And the quote referencing their duelling abilities was my point. Considering that dueling abilities are related to 2 things, augmentation and technical skill. Augmentation is directly related to one’s raw power in the force, and therefore since Kenobi’s skill as a duelist has regressed, his force power has likewise. Since you’ve not responded to my claim that Vader’s comment that “your powers are weak, old man”, means that Kenobi’s powers have regressed since ROTS, I’ll take that as a concession.
There is a fundamental difference between augmentation and raw force power, especially in a vessel as old as Obi-wan. Also, being a shadow of Mustafar Kenobi that can contend with Anakin is not at all bad. Consider the kind of growth Kenobi must gain throughout Revenge of the Sith and juxtapose that with the unquantifiable deterioration he experienced. Now, try and prove that Ben who is compared to his prime self is beneath the Kenobi who was making Dooku sweat on the Hand.
Again, you cannot have read my first post and written this. I addressed “your powers are weak old man” as Vader’s drain, he says this to Kenobi after he overpowers him. They stand for minutes just staring at one another and Kenobi begins to sweat, then Vader says that line: “your powers are weak old man”
IG wrote:Except Luke makes an earnest attempt at lifting the X-Wing and fails utterly. His confidence or lack thereof in his abilities doesn’t change the fact that this kind of TK is something he deems beyond himself with good cause--he simply cannot do so.
You aren’t reading my quotes at all, that’s all but confirmed now.
“Because luke does not believe it is possible, he fails to raise the ship.”
That statement attributes Luke’s lack of confidence as the reason he can’t lift the ship, it’s asinine that you would argue this point considering, as you said earlier; Luke can tag Vader and is out of his ragdoll range. If you truly think that Luke shares some relativity with ESB Vader then you must admit that he is above ANH Vader via his comparison with Ben, who is at least more powerful than Dark Times Vader who is capable of exceeding the X-wing feat only a few months after Revenge of the Sith:
Even if you are right about Vader’s growth and he only grew one ragdoll gap from 19-18bby that still means ANH Vader ragdolls this Vader and ANH Vader and ESB Vader have a large gap that Luke has to not be in ragdoll range from. In layman's terms (since it might be easier if I dumb this down for you) arguing Vader struggles with someone who can’t lift a small ship is fallacious and against the actual lore provided.
IG wrote:
Characters grow only through conflict, per Kreia. Considering that Dooku is involved in a massive galactic scale war, it’s pretty obvious that he grows a lot. Consider also that Dooku throws the ships and cruiser “with ease”. My comparison was simple, that Dooku’s TK is far, far beyond ESB Luke’s. Dooku being able to casually throw around cruisers (while amped, yes) and then undergoing 3 years of immense growth is a testament to his power. You haven’t sufficiently demonstrated that the nexus of Korriban circa 22 BBY is strong enough that it means Dooku cannot throw cruisers around when not amped by it. Perhaps when not amped by Korriban Dooku won’t be throwing ships around with such casual ease. My point remains however, that Dooku’s TK is demonstrably far beyond what Luke as of ESB has shown.
No your “comparison” was a gross misinterpretation of the lore for the sake of lowballing. I gave you two quotes attributing his failure to lift the X-wing to his belief in his own abilities and you tried to handwave them away by citing his response; “it’s impossible”...
No shit he thinks it’s impossible, that is why he can’t lift the damn thing in the first place.
Good on you for entirely conceding your point about the weakness of Korriban’s nexus relative to the EmpalSuRecon though. I’m impressed you can suppress your ego enough to admit you are wrong.
IG wrote:To put (someone or something) to the test is defined as “to cause (someone or something) to be in a situation that shows how strong, good, etc., that person or thing really is”. Meaning that Yoda is the only one thus far that has shown how strong Dooku really is. That doesn’t mean Anakin couldn’t have pressed him though. Toying with one explicitly means that you’re playing around with them to amuse yourself. Dooku is pressed by Anakin to a degree, but it isn’t something that makes Dooku utilize his full ability.
So you agree he’s still not tested and doesn’t give it his all right? I don’t care how much he was or was not holding back, we know he was toying:
Wild Space wrote:On the floor of the cavern on brutal Geonosis, rendered helpless by two lightsaber cuts, he watched Dooku toy with bold, rash Anakin. Silver hair gleaming, teeth bared in a smile, the ageless Sith, the treacherous Jedi, prowled around Anakin with insolent ease. Deflected each blinding attack with casual, consummate skill. Forced the error-and took Anakin's arm.
Since we do agree he is toying and Kenobi and fact files supports this idea, it’s easy to say that him not being tested and engaging in two short lightsaber duels and getting tired is indicative of his poor stamina. The flashes of brilliance clearly don’t press him, because he is not “tested” as you so adequately described.
You implied that you had definitive proof that Dooku can exhaust Dooku due to his skill. Yoda “lacks the stamina of youth” and literally has arthritis and needs a cane to walk. In order to duel he uses the most physically exhausting form bar Juyo so of course after he deactivates his force reserves he will feel fatigue. This means nothing.
IG wrote:And I see no reason for said feats of strength to be referring to raw power in the force. Like, we clearly see Anakin being far superior to Vader in terms of the force, and there’s no reason that Vader’s cybernetic enhancements should make up that gap. Your argument that Vader jumps a ragdoll gap a year clearly falls flat when we take into account the fact that if in 19 BBY, Vader with aug + cybernetics > Anakin with Aug, then by 4 BBY, he should be tossing around the PT Titans with ease.
You straight up ignored my entire argument. Like, I can only assume this is willful ignorance because I can’t fathom this level of stupidity. The feats of strength Vader can perform as a cyborg are far greater than that of Anakin. This is literally compared to having very little access to the temples records, to having all of it at his fingertips from across the galaxy, which denotes it’s a huge gap. His augmentation and powerlevel means jack shit when he himself says that the feats he can perform now are better.
IG wrote:For your point about Mace fighting Dooku: it’s fairly evident from how short the fight is (literally one or two exchanges) that Mace can’t get a feel for Dooku’s strength from it.
You argue this now, yet argued earlier his contention with mace was a showing placing him above the likes of Kenobi. To quote you: “Your double standards astound me.”
IG wrote:
Considering Dooku’s fought on par with the likes of Yoda and not yielded in bladelock, your claim that Vader can physically overpower Dooku when Vader’s already shown himself to be much weaker than Yoda is incorrect.
You haven’t drawn any connection between Vader being physically inferior to Yoda or why.
IG wrote:Considering that I've given and backed up evidence for why Vader <= AOTC Anakin, I think it's safe to say that no, Vader isn't striking with "more deadly invincibility" in that comic.
You haven’t backed anything up yet and Vader can still be stronger than AOTC Anakin by your quote, why must you chastise me for arguing something you have yet to even address?
 The Fallen WarriorLevel Four
The Fallen WarriorLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:14 pm
Section III - Inferiority to Yoda, Reaffirmed
Have you even read any of my quotes? Prove he can sense force signatures during his flow-walking.
He could just be saying that Anakin’s potential is greater but even if he wasn’t, possibly denotes uncertainty. I gave you many quotes saying Yoda was the most powerful Jedi as of Revenge of the Sith and you made the claim he was equal to, or more powerful than Yoda. You have failed at explaining why this is the case.
In the quote I provided:

Ah, so given this new evidence and my quote, we can conclude that the 9 is in reference to when he gives into the Darkside, yet he still starts the film as an 8.
Once again:


Vjun is a Darkside nexus and those who are connected to the lightside of the force find their powers “diminished” while those who wield the dark side are “amazed at the strength they gain.” Essentially, I already proved Yoda is not full DS and Yoda actively resists the nexus earlier in the book:
With all this evidence, we return the fact we know that Yoda and Dooku have an “enormous gap” by Revenge of the Sith and Dooku is relativistic to Kenobi, so it is far more likely and fits better with the lore for Yoda to be hindered while Dooku is amped. If you still aren’t convinced, Yoda and Dooku's dialogue in the duel suggests he is actively resisting the darkside:
Dooku is trying to goad Yoda into giving into his hate, which Yoda clearly has not done at this point in the duel, this is after the line “in the dark, drunken Vjun air, Yoda was terrible to behold.” Which means that Yoda has not given into the Darkside and by definition of being a lightsider on a “Dark Side Site” such as Vjun, Yoda would find his powers “diminished.”
The “even here on Vjun” is very important as it insinuates that the Darkside is trying to corrupt him hence the “whispering” but he chooses to “love” signifying his resistance to all those “whispers.” Here we see Yoda repel all the anger he feels, but we know he has not yet used it or Dooku wouldn’t have been goading him to give into his anger. If Yoda does give into the Darkside at some point like I said it is a hindrance because Yoda is not shown capable of using the light and dark sides in tandem and thus the two would be clashing, which ends up “poisoning” him. Notice how after he calms himself, we see Yoda immediately drive Dooku back and almost end the duel outright:
The most damning bit of evidence comes from the end of the duel:
Yoda chooses not to “annihilate him utterly” and he has to resist the urge, which again means he isn’t drawing on it, the allusions to the air are of it’s corrupting nature not that he is drawing on it's power.
The quote says that Yoda “tapped in” and that one “could” use it like waves. But we must question what Stewart really meant by the “expert surfer.” Initial thoughts lead us to conclude it’s Yoda; he’s older, wiser, and more powerful. Yet the context of the quote is that it’s the expert and novice on Vjun. With this in mind, who has more experience actively weidling the darkside? Who would be the “expert” at “doing more with that (darkside)” power. Well obviously it would be Count Dooku. This makes sense in the context of the duel since the proverbial darkside “novice” (Yoda) is in a situation where it’s “easier for him to lose control.” We see several times where Yoda actively resists the temptation of the Darkside, and during a fight where one has to be focused on the opponent a distraction such as this that “diminishes” his power, would surely hinder him.
Perhaps you are simply oblivious to what Insider was promoting at this time. Each issue was a “sneak peak” of what was to come in Revenge of the Sith, which is even implied in one of Hidalgo’s answers to a Q & A at this time:


It’s also telling that he deliberately uses the statement “Anakin as a young man” instead of referencing Attack of the Clones. The vagueness of the quote combined with what Insider was at the time “a sneak peek” means it could easily be referring to Revenge of Sith Anakin
Just saying it is not the equivalent of proving it. I gave you a source claiming that most of the filming was done at this time, I explained that the time period it was released in could easily be referring to Revenge of the Sith Anakin. You have just repeated the same thing without evidence.
The audience's perception is not OOU. Tell me why I should give a damn what Billy Bob thinks about the movies?
These quotes could all easily be referencing technical skill. Vader is not the most technically skilled, as you said “he lacks the polish of study with lifelong masters” comparatively Luke’s style is emulated based off of Vader’s but we know that their styles while not as flashy or sophisticated as the PT Jedi allow them to contend.
Vader is the connective tissue to which all things regarding PT vs OT revolve around. If every single PT Jedi were a far greater combatant than Vader why is it that he became known for hunting and murdering them during the purge? How do you reconcile Vader being a terrible duelist that has no relativity to any of the PT Jedi we see, yet he consistently bests them? If you want an example; Roan Shryne and Maki’is are both background characters in Attack of the Clones and Revenge of the Sith respectively, which means that we have “seen them." Vader duels even with Roan Shryne before his faith in the dark side is “firmed” as you quoted. So how come Vader can two-shot Makis in Purge? The only reasonable explanation is that while Vader is not as flamboyant or acrobatic as the Jedi of the prequels and is “an old man” and “half robot” he still possesses the skills and powers to contend and even win a majority of the time. Similarly Ben is not acrobatic or flamboyant, but we know that his skill with a lightsaber was still very deadly.
These quotes also have their own contradictions. For instance Lucas cites Obi-wan being “ready to drop” as the reason that his skill has deteriorated so far, yet ironically enough Dooku is canonically older than Ben, which by Lucas’s and your logic means he would be “frankly shit.”
This to me seems like an overcompensating attempt to lowball Vader with things that just don’t make sense when you try to fit them into the lore.
Section IV - Circular Logic
Force lightning is hard to deflect by nature of it’s very properties:

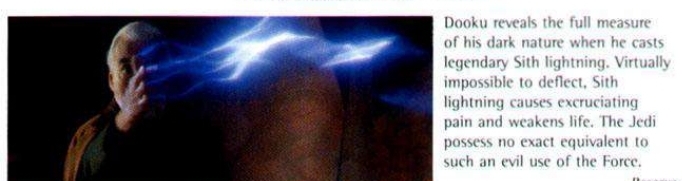
Yoda having difficulty deflecting it with tutaminis is unsurprising considering that it causes “excruciating pain” and even the “most powerful jedi masters” are “challenged” by deflecting it. This is not a showing of parity whatsoever.
As for your point about Galen’s lightning, that's not how this works. You used Galen’s lightning as your baseline for why Dooku can do the same, I simply asked you to quantify why you think Dooku has as potent of lightning as Starkiller. I don’t have to draw comparisons of power between the two since I wasn’t the one who made the claim. All you did was go in a circle here, provide a connection for why Dooku can do what Starkiller can, the burden of proof is on you.
Your interpretation of the lore simply does not fit as well as mine. I have tried tirelessly to explain that due to the Gillard tiering system the gap between Yoda and Dooku is gargantuan, and due to Yoda’s parity with Sidious a being who is “beyond power” to Dooku’s perception there is no hope of Dooku catching up by Revenge of the Sith, And the fact that Kenobi is relativistic to Dooku means Yoda is vastly beyond him anyway. That leaves us with three options. Either:
-Dooku has all these great showings but with stipulations attached so that Yoda is not as powerful as he would be as a nine.
-Dooku has very specific advantages against Yoda that won’t be there against Vader.
-Or, Yoda experiences some great amount of growth in the period between YDR and Revenge of the Sith that renders the entire comparison moot.
Did I ever deny Ben’s inferiority to his Mustafar “letting go” form? My argument was built around the premise that the level of deterioration he experienced was canceled out by the growth he shows throughout Revenge of the Sith. Luke does have more raw power then Ben, you would know that if you actually read my quotes. He is also more skilled, something I’ve already substantiated that you seemed to ignore.

This is not a merry go round IG. When I say something, you parroting it back to me deflecting the burden of proof off of you just doesn’t look good. I asked you to give me substance on why I should believe the quote only could refer to Attack of the Clones Anakin and not Revenge of the Sith. Your response thus far has been insubstantial.
No. You see my young friend, the reason Luke cannot lift the X-wing is noted to specifically be his lack of faith in his abilities. It’s not that Luke doesn’t think he can do it, that’s not what I’m arguing. I’m saying that two quotes support the notion that Luke cannot lift the X-wing due to his own mindset. That’s it. To quote the Revenge of the Sith novelisation.
The war growth would go for Vader as well. If you are genuinely arguing that Dooku grows powerful enough to circumvent the Korriban nexus, my ragdoll tier gaps should be perfectly reasonable. That aside, you have yet to substantiate that unquantifiable growth as reason enough for us to assume he can perform that level of TK on average.
So, why would Vader not use a barrier if he is aware of his weakness to lightning? Why would he try to counter it with something he knows is ineffective. Against the Starkiller clone he was facing an equal, so it makes sense that the bursts would get through on chance occasions, but even then all it did was slow him down. Prove to me why Dooku is on Starkiller’s level lightning wise and prove to me how this weakness is so absolute that it assures Dooku victory. Then articulate why Dooku’s dueling skills are so exorbitantly above Vader’s that he can mitigate Vader’s colossal strength advantage and superior durability, or why Dooku is able to just ragdoll him outright and why that would stop Vader.
Section V - Old Man vs Sith Terminator
That’s one way things could happen. Another is what happened during The Force Unleashed (which is far closer to the mature Vader I am debating with) where Vader’s attacks “redouble” and he becomes infinitely more deadly. Wouldn’t it be equally likely things played out as they did on the Invisible Hand but this time Dooku’s taunt backfired causing Vader to get mad and simply overpower him?
Okay, ironically enough you validate my points about Yoda here with Zannah’s quote describing how exhaustive Ataru is. Then you go on to push for this parity to Yoda during the duel which you have yet to describe as anything more than being pushed back for 40 seconds. Again you argue that Anakin is a “Yoda+” to which I raise you the numerous quotes I posted last time claiming Yoda was stronger in the force. To top it off you completely ignored my argument about Dooku getting tired. I don’t care if Anakin had “flashes of brilliance” when we know it was “easy” for Dooku to dismantle both Kenobi and Anakin individually.

This weakness would only get worse by Revenge of the Sith as Dooku notes his body has further physically deteriorated by the time he’s onboard the Invisible Hand:
Dooku doesn’t have the stamina to keep up with Anakin’s blows spending “lavishly his every reserve” just to survive. So, while you can argue all day long about Dooku’s stamina with Yoda, how exhausted he was, Anakin who is not as physically dominating as Vader was already “aging him with every blow.”
Conclusion
You literally conceded your entire “definition of sport argument” how does every point still stand? How is ESB Luke inferior to Ben when the very nature of your argument is that Augmentation = Power in the force? George Lucas himself has stated that the lightsaber fighting kept improving in every film, and you clearly subscribe to those statements. This is more than a double standard, it’s as you so freely call my arguments: “insane”
As long as the quote has any alternative interpretation, as I have shown it does, you cannot prove that.
The nature of force lightning is the reason that Yoda had difficulty with it, you established no direct link to Galen Marek, this does not work.
Or just piss him off further making him more powerful and aggressive.
Not against people with Anakin+ tier strength.
All I was trying to explain was that the gap between them wasn’t that large and that Vader’s growth combined with Luke’s superiority to Ben who has power in the same realm as his ROTS self, perhaps even on par with his IH Kenobi self, means that Vader can compete.
Based on Kenobi’s “instantaneous reactions?” Is this a joke? You haven’t substantiated one claim I made about this, the baseline being that Dooku cannot effortlessly handwave Kenobi away with a ragdoll nor can he engineer a situation that allows him to do so. It was a conscious decision for Kenobi not to erect his barrier and a tactical failure, but it was not a showing of superior power.
Let’s weigh the two shall we?
They both have power to suggest neither can ragdoll the other.
For team Tyranus we have:
For Team Vader we have
You can clearly see that one set of advantages cancels out the other. It’s like the ROTS Novel says:
IG wrote:
Have you read Bloodlines? Caedus flow-walked into the past. He basically time-travelled, to be concise. He isn’t going off of old records and what Luke could tell him, evident from Caedus witnessing a scene that there is likely no record of--Anakin being denied mastery.
Have you even read any of my quotes? Prove he can sense force signatures during his flow-walking.
IG wrote:Except this isn’t referring to Anakin’s potential whatsoever. Sidious didn’t say “Anakin has the potential to be stronger than myself”. Sidious says that as of that minute, Anakin is possibly stronger than himself.
Revenge of the Sith wrote:
"He is powerful. Potentially more powerful than even myself."
He could just be saying that Anakin’s potential is greater but even if he wasn’t, possibly denotes uncertainty. I gave you many quotes saying Yoda was the most powerful Jedi as of Revenge of the Sith and you made the claim he was equal to, or more powerful than Yoda. You have failed at explaining why this is the case.
IG wrote:Where does Gillard ever claim Anakin starts ROTS as an 8?
In the quote I provided:
IG's quote
"Hayden Christensen is one of the best there is," says Gillard. "I've seen hundreds of sword fighters, people who do it for a living, and he leaves them all in his wake. His style has changed a bit since Episode II, when he was only a level seven. On this he's a level nine."
Ah, so given this new evidence and my quote, we can conclude that the 9 is in reference to when he gives into the Darkside, yet he still starts the film as an 8.
IG wrote:Yoda is actively drawing upon the dark side throughout this fight. It’s pretty evident in the book itself. “In the dark, drunken Vjun air, Yoda was terrible to behold”. “And yet, even here on Vjun, where the dark
side whispers and whispers to me...love you enough to destroy you I do”.
Yoda utilizing the dark side doesn’t mean that he’d be hindered or conflicted. There’s nothing that actually hints at conflict. Yoda states he’s going to kill Dooku, and that the DS “whispers and whispers” to him. Given that you’re using the author quote over there, I think that means that you really won’t object to my use of it as well. And Stewart explicitly states, “so my instinct would be that he’s tapped into Vjun”, and that “Yoda and Dooku are both like surfers in a place with big waves. The more expert the surfer, the more they can do with that power”. Meaning that Yoda is utilizing the nexus of Vjun to a greater effect than Dooku is, but he’s only pushing him back, “slowly, slowly”.
Once again:
Vjun is a Darkside nexus and those who are connected to the lightside of the force find their powers “diminished” while those who wield the dark side are “amazed at the strength they gain.” Essentially, I already proved Yoda is not full DS and Yoda actively resists the nexus earlier in the book:
Yoda: Dark Rendezvous wrote:Yoda was close by. He was moving carefully, quietly, hiding his presence in the Force; riding on its back like a leaf whirled gently down a stream. But on Vjun, the Force was bent mightily to the dark side, and every now and then the Master opposed its current. It was these moments Dooku was listening for. Once, several minutes ago, the old Jedi had misstepped, putting a foot against the current, and the shock of it had rumbled through the very bedrock beneath Château Malreaux, announcing the Master's coming like a distant groundquake. Or maybe it hadn't been a mistake. Maybe Yoda wanted Dooku to know he was on his way. Since then the world had been silent. The old Jedi was moving like a water-skeeter over the surface of the Force, with nothing to herald his coming but a faint sensation of heat on Dooku's skin, as if he were a blind man at sunrise, the dawn invisible to him but for a pale, spreading warmth.
With all this evidence, we return the fact we know that Yoda and Dooku have an “enormous gap” by Revenge of the Sith and Dooku is relativistic to Kenobi, so it is far more likely and fits better with the lore for Yoda to be hindered while Dooku is amped. If you still aren’t convinced, Yoda and Dooku's dialogue in the duel suggests he is actively resisting the darkside:
Yoda: Dark Rendezvous wrote:"Yes," Dooku whispered. "Feel me. Feel the treason. All those years of teaching me, raising me. Trusting me. And here am I, the favored son, butchering your precious Jedi, one by one. Hate me Yoda. You know you want to."
Dooku is trying to goad Yoda into giving into his hate, which Yoda clearly has not done at this point in the duel, this is after the line “in the dark, drunken Vjun air, Yoda was terrible to behold.” Which means that Yoda has not given into the Darkside and by definition of being a lightsider on a “Dark Side Site” such as Vjun, Yoda would find his powers “diminished.”
Yoda: Dark Rendezvous wrote:
Dooku brought his blade down toward the diminutive Jedi Master and Yoda parried, locking his blade against Dooku's. Yoda breathed, calming himself. "And yet, even here on Vjun, where the dark side whispers and whispers to me . . . love you enough to destroy you I do."
The “even here on Vjun” is very important as it insinuates that the Darkside is trying to corrupt him hence the “whispering” but he chooses to “love” signifying his resistance to all those “whispers.” Here we see Yoda repel all the anger he feels, but we know he has not yet used it or Dooku wouldn’t have been goading him to give into his anger. If Yoda does give into the Darkside at some point like I said it is a hindrance because Yoda is not shown capable of using the light and dark sides in tandem and thus the two would be clashing, which ends up “poisoning” him. Notice how after he calms himself, we see Yoda immediately drive Dooku back and almost end the duel outright:
Yoda: Dark Rendezvous wrote:
Pushing Dooku back yet again, blades flashed and flared stutters of light, blood red and sea green.
Sweat ran in streams through Dooku's beard as he countered Yoda's every move, and his lips were white. Holobattles raged around them as the consoles showed Obi-Wan and Anakin clashing with wave after wave of battle droids. Dooku shot a quick glance at the red button on his desk and, with a Force push, he punched it in.
The most damning bit of evidence comes from the end of the duel:
Yoda: Dark Rendezvous wrote:
And with that he leapt backward, out the window. Yoda bounded after him. In the dark Vjun air it was all he could do not to leap after Dooku, to fall on him like a green thunderbolt and annihilate him utterly.
Yoda chooses not to “annihilate him utterly” and he has to resist the urge, which again means he isn’t drawing on it, the allusions to the air are of it’s corrupting nature not that he is drawing on it's power.
IG wrote:Given that you’re using the author quote over there, I think that means that you really won’t object to my use of it as well. And Stewart explicitly states, “so my instinct would be that he’s tapped into Vjun”, and that “Yoda and Dooku are both like surfers in a place with big waves. The more expert the surfer, the more they can do with that power”. Meaning that Yoda is utilizing the nexus of Vjun to a greater effect than Dooku is, but he’s only pushing him back, “slowly, slowly”.
The quote says that Yoda “tapped in” and that one “could” use it like waves. But we must question what Stewart really meant by the “expert surfer.” Initial thoughts lead us to conclude it’s Yoda; he’s older, wiser, and more powerful. Yet the context of the quote is that it’s the expert and novice on Vjun. With this in mind, who has more experience actively weidling the darkside? Who would be the “expert” at “doing more with that (darkside)” power. Well obviously it would be Count Dooku. This makes sense in the context of the duel since the proverbial darkside “novice” (Yoda) is in a situation where it’s “easier for him to lose control.” We see several times where Yoda actively resists the temptation of the Darkside, and during a fight where one has to be focused on the opponent a distraction such as this that “diminishes” his power, would surely hinder him.
IG wrote:Except Revenge of the Sith wasn’t released yet. Until something is published (released in this scenario), it has no canonical validity. There’s a reason that Supernatural Encounters isn’t canon, it isn’t published. Meaning that by default, Hidalgo is referring to AOTC Anakin because Revenge of the Sith just doesn’t exist yet as a canonical entity.
Perhaps you are simply oblivious to what Insider was promoting at this time. Each issue was a “sneak peak” of what was to come in Revenge of the Sith, which is even implied in one of Hidalgo’s answers to a Q & A at this time:
It’s also telling that he deliberately uses the statement “Anakin as a young man” instead of referencing Attack of the Clones. The vagueness of the quote combined with what Insider was at the time “a sneak peek” means it could easily be referring to Revenge of Sith Anakin
IG wrote:Well skill is directly related to power. Anakin’s technical skill + aug/raw power are what define his skill, and those two elements define Vader’s skill as well. Since I’ve established that the quote does indeed refer to AOTC, we can determine from it that Vader’s raw power is equivalent (if not less than) the raw power that AOTC Anakin possesses. Hell I can even be generous and say his raw power is on par with that of a “flash of brilliance” AOTC Anakin. But we’ve seen how both of those fights go--not a very good outcome for Vader, really.
Just saying it is not the equivalent of proving it. I gave you a source claiming that most of the filming was done at this time, I explained that the time period it was released in could easily be referring to Revenge of the Sith Anakin. You have just repeated the same thing without evidence.
IG wrote:Except the quote’s explicitly referring to something OOU. It’s declaring that audiences will perceive Luke as “not that powerful” compared to one such as AOTC Yoda, for example. It’s a declaration of intent, to start. It’s a quote that has backing in several sources, such as the ones below:
The audience's perception is not OOU. Tell me why I should give a damn what Billy Bob thinks about the movies?
PT versus OT Quotes wrote:“We will finally get to see Jedi do what Jedi were designed to do. In the first one, you had this very old Jedi who was ready to go, and one who had been reconstructed who was half human and half machine. The only other Jedi who comes along is Luke, who is sort of semi-trained by Yoda, but never really gets the full training. So you’ve never seen a real Jedi doing what the real Jedi do, until now.” - George Lucas
Until the Prequels, the only Jedi we’d seen in combat were old men and an inexperienced youth… and clearly, we hadn’t seen anything.
Star Wars Insider Magazine #131 wrote:
Before this scene, the lightsaber battles we’d seen in the Star Wars movies involved older Jedi, or Jedi who were yet to become full-fledged Jedi Knights, but here we saw Jedi and Sith fighting when they were at the top of their game.
Starwars.com - Homing Beacon #57 wrote:
"We're trying to go much more classical for some characters," says Gillard, "Some of the characters are real master swordsmen, better than anything we've seen so far. So we're using an old, classical European style for a couple of the characters." - Nick Gillard
These quotes could all easily be referencing technical skill. Vader is not the most technically skilled, as you said “he lacks the polish of study with lifelong masters” comparatively Luke’s style is emulated based off of Vader’s but we know that their styles while not as flashy or sophisticated as the PT Jedi allow them to contend.
Vader is the connective tissue to which all things regarding PT vs OT revolve around. If every single PT Jedi were a far greater combatant than Vader why is it that he became known for hunting and murdering them during the purge? How do you reconcile Vader being a terrible duelist that has no relativity to any of the PT Jedi we see, yet he consistently bests them? If you want an example; Roan Shryne and Maki’is are both background characters in Attack of the Clones and Revenge of the Sith respectively, which means that we have “seen them." Vader duels even with Roan Shryne before his faith in the dark side is “firmed” as you quoted. So how come Vader can two-shot Makis in Purge? The only reasonable explanation is that while Vader is not as flamboyant or acrobatic as the Jedi of the prequels and is “an old man” and “half robot” he still possesses the skills and powers to contend and even win a majority of the time. Similarly Ben is not acrobatic or flamboyant, but we know that his skill with a lightsaber was still very deadly.
These quotes also have their own contradictions. For instance Lucas cites Obi-wan being “ready to drop” as the reason that his skill has deteriorated so far, yet ironically enough Dooku is canonically older than Ben, which by Lucas’s and your logic means he would be “frankly shit.”
This to me seems like an overcompensating attempt to lowball Vader with things that just don’t make sense when you try to fit them into the lore.
Section IV - Circular Logic
IG wrote:
Here I’m only citing this one part of your post because I’m not going to cite every small portion, but don’t take this as a concession, I’m countering every relevant part of that post.
While Barriers and Lightning can block lightning, it’s stated that Yoda deflected Dooku’s lightning “far from easily”. Dooku is capable of blasting Anakin back with his lightning while being held in a chokehold and in saberlock (link ).
You also haven’t provided evidence for why SK’s lightning is on par with Dooku’s. Given Dooku’s capable of pressing Yoda with his lightning, there’s not really evidence for why SK’s lightning is that much better than his.
Force lightning is hard to deflect by nature of it’s very properties:
Yoda having difficulty deflecting it with tutaminis is unsurprising considering that it causes “excruciating pain” and even the “most powerful jedi masters” are “challenged” by deflecting it. This is not a showing of parity whatsoever.
As for your point about Galen’s lightning, that's not how this works. You used Galen’s lightning as your baseline for why Dooku can do the same, I simply asked you to quantify why you think Dooku has as potent of lightning as Starkiller. I don’t have to draw comparisons of power between the two since I wasn’t the one who made the claim. All you did was go in a circle here, provide a connection for why Dooku can do what Starkiller can, the burden of proof is on you.
IG wrote:As I’ve already proven, Dooku is relativistic to a nonhindered version of Yoda, and he’s dismissing Kenobi with ease when not pressed by Skywalker simultaneously and/or in a state of stupor
Your interpretation of the lore simply does not fit as well as mine. I have tried tirelessly to explain that due to the Gillard tiering system the gap between Yoda and Dooku is gargantuan, and due to Yoda’s parity with Sidious a being who is “beyond power” to Dooku’s perception there is no hope of Dooku catching up by Revenge of the Sith, And the fact that Kenobi is relativistic to Dooku means Yoda is vastly beyond him anyway. That leaves us with three options. Either:
-Dooku has all these great showings but with stipulations attached so that Yoda is not as powerful as he would be as a nine.
-Dooku has very specific advantages against Yoda that won’t be there against Vader.
-Or, Yoda experiences some great amount of growth in the period between YDR and Revenge of the Sith that renders the entire comparison moot.
IG wrote:Dooku is definitely > a Kenobi that had ample opportunity to muster his defenses. I’ve sufficiently shown Ben’s inferiority to his ROTS iteration per a wealth of sources, including George Lucas himself. While Luke may have combatative skill above that of Ben, that doesn’t preclude having more raw power, and your “ragdoll gap a year jumping” argument doesn’t stand anymore.
Did I ever deny Ben’s inferiority to his Mustafar “letting go” form? My argument was built around the premise that the level of deterioration he experienced was canceled out by the growth he shows throughout Revenge of the Sith. Luke does have more raw power then Ben, you would know that if you actually read my quotes. He is also more skilled, something I’ve already substantiated that you seemed to ignore.
IG wrote:No reason to believe it doesn’t refer to his AOTC iteration, so this is a baseless claim.
This is not a merry go round IG. When I say something, you parroting it back to me deflecting the burden of proof off of you just doesn’t look good. I asked you to give me substance on why I should believe the quote only could refer to Attack of the Clones Anakin and not Revenge of the Sith. Your response thus far has been insubstantial.
IG wrote:Luke may find the task impossible, but he also is incapable of doing so as well. Him not thinking he can do something doesn’t mean he automatically won’t be able to. Luke deems the task impossible because it is something he deems beyond his own abilities, something he should be an accurate gauge for at the time.
No. You see my young friend, the reason Luke cannot lift the X-wing is noted to specifically be his lack of faith in his abilities. It’s not that Luke doesn’t think he can do it, that’s not what I’m arguing. I’m saying that two quotes support the notion that Luke cannot lift the X-wing due to his own mindset. That’s it. To quote the Revenge of the Sith novelisation.
Revenge of the Sith wrote:It is that simple and that complex.
IG wrote:You’ve yet to substantiate why Dooku’s amp isn’t mitigated by the fact that he’s capable of throwing the ships easily and war growth. To reiterate that argument, even if Dooku can’t throw the ships with ease after he has no nexus amp, he’ll still be able to throw them to some degree, if we account for war growth. To contrast, Luke has nothing putting him near that level of TK
The war growth would go for Vader as well. If you are genuinely arguing that Dooku grows powerful enough to circumvent the Korriban nexus, my ragdoll tier gaps should be perfectly reasonable. That aside, you have yet to substantiate that unquantifiable growth as reason enough for us to assume he can perform that level of TK on average.
IG wrote:Dooku’s lightning is capable of giving Yoda difficulty. Given tutaminis is a better counter for lightning than a barrier (energy absorption vs using TK to create a protective bubble), it makes sense that Vader will be incapable of defending against lightning that’s pressing Vader’s vast superior in Yoda with a barrier, an inferior form of lightning defense than tutaminis. As for using a saber, I’ll be responding to that in my next section.
So, why would Vader not use a barrier if he is aware of his weakness to lightning? Why would he try to counter it with something he knows is ineffective. Against the Starkiller clone he was facing an equal, so it makes sense that the bursts would get through on chance occasions, but even then all it did was slow him down. Prove to me why Dooku is on Starkiller’s level lightning wise and prove to me how this weakness is so absolute that it assures Dooku victory. Then articulate why Dooku’s dueling skills are so exorbitantly above Vader’s that he can mitigate Vader’s colossal strength advantage and superior durability, or why Dooku is able to just ragdoll him outright and why that would stop Vader.
Section V - Old Man vs Sith Terminator
IG wrote:Ferus Olin bringing up Padme’s name to Vader makes Vader go batshit. Dooku has knowledge of Anakin’s “messy private life”, and therefore will have an ability to make Vader go into a rage, in which he will leave more openings that Dooku can exploit with ease, as Dooku’s shown himself quite proficient in that regard, through his ability to create openings in his fight with Kenobi and Skywalker and exploit them.
The Last of the Jedi: Reckoning wrote:
Ferus saw the glow of Vader's lightsaber as he activated his own.
This was it, then. The final confrontation.
He was ready. His rage was ice and fire.
He charged.
His first blow was easily parried. He came at Vader again. Again. Circling, jumping, vaulting past him, turning. Each time his lightsaber came toward him, it was eilher deflected in a shock that ran up his arm, Vader simply wasn't there.
"If you cannot even touch me, how can you win?" Darth Vader asked.
Ferus focused on his anger. He remembered Palpatine's words.
There is no limit to what you can do.
He charged at the dark figure again. This time his strike came close. He touched the edge of Vader's cape. He smelled the singed material.
Now, while he's off balance. Now.
"Maybe I'll just get lucky," Ferus said. "Anakin."
Vader came at him with surprising swiftness, but Ferus was able to Force-leap away. Still he sensed that Vader was holding himself back, playing with him for now.
"So you know who I was," Vader said. "Do you think that would make a difference to me? Anakin Skywalker is dead."
"Was it because the Council wouldn't let you become a Master? You always had to struggle with your ego, didn't you?"
"It was never a struggle. I was always the best."
" 'Best' is not a Jedi concept."
"That is the trouble with the Jedi."
Ferus wasn't tired yet, but he knew he was expending too much energy. He was tapping into his anger and fighting better than he ever had, but it wasn't enough. He had to unsettle Vader. He had to find the key.
He had everything he needed to defeat him, didn't he? He had the Sith Holocron for strength, Vader's true identity in his hand, his own rage. With those tools, he could do it. The Emperor had told him he could. Ferus thought quickly. He wanted to pick the battleground. Someplace that would unsettle the former Jedi.
There - the stairway to the Jedi High Council spire. Ferus started to climb. He knew Vader would follow.
He came out into the circular room. It was half rubble, the seating blackened lumps, the vast transparisteel shattered. Wind whipped through the room.
The Dark Lord entered. The wind blew back his cape. He stood, legs apart, ready for battle. Looking forward to it, Ferus was sure.
"The Emperor cannot protect you now," Vader said.
What next? What could Ferus do to get him off balance? He suddenly had a flash of intuition. He remembered what Keets had told him.
"What about Senator Amidala?" he asked, leaping away from Vader. He faced him, his lightsaber held in an offensive position. "What about Padme? What happened on Mustafar?"
He felt the quake in Vader. He had reached him at last.
"Do not mention her name!"
"I thought it was a lie, that the Jedi killed her," Ferus suddenly understood, the Sith Holocron burning under his tunic. "ft wasn't. You killed her, didn't you? You killed the woman you loved."
Vader's wrath filled the room. Ferus could feel it. Instead of turning away from it, he took it. He filled himself with it.
This is what the Emperor meant. This is the last step.
He flew across the room and this time he landed a blow.
Vader roared. It was a howl of fury, inarticulate, undisciplined. Totally unlike his usual icy control. The control box on his chest started to smoke.
Stones in the floor ripped out and were flung toward Ferus. He dodged them, rolling and twisting away. A blackened piece of furniture flew across the chamber and smashed into the wall over his head.
Anything that could be torn from the floor or walls came at him - conduits, debris, hunks of stone. He dodged and weaved, attacking and retreating as Vader hit him with everything he had.
"How did you kill her, Anakin? Did you lose control? Did you see her die, Anakin? Is that why you wanted Zan Arbor to perfect that drug? Was it for you, Anakin? So you could forget her? So you could forget your wife?"
Another roar from Vader. part of the ceiling gave way. Durasteel melted, smoke rose from the debris. Ferus leaped over a gaping hole in the floor and attacked Vader again, but his lightsaber cut through empty air.
The anger inside Ferus was now like liquid fuel inside him. He was feeding off Vader's rage, he was pushing every molecule of his body and feeling every molecule of the room respond to him. Everything was clear, hard-edged. His body obeyed him without any hesitation, and his mind was focused. He had no doubt that he could defeat Vader. No doubt.
And that was what the dark side brought him.
When he won, when he defeated him, he could take the victory to the Emperor, and he could be greater than Darth Vader, more powerful than even the Chosen One had been.
He charged at Vader and made contact. Vader waited a beat too long to deflect him. The blow shuddered off his body arrnor. Something inside fused and the plastoid melted. Ferus could smell buming circuits. At the same time, he detected a tremor in Vader's arm.
Suddenly he was picked up and slammed against the wall. He fought to hold onto his consciousness.
"Don't . . . get . . . cocky," Vader said.
Ferus rolled away from the blow that followed, barely escaping. He looked up. For a moment Vader was just a shape at the side of the room. For a moment, a trick of the eye or the light, he saw the room as it had been. The seats were restored, the air traffic outside flashing, the potent energy of the Force filling the room because the Jedi Masters were still alive.
Ferus felt it invade him, the sense of peace and light.
No, push it away! Listen to us! You could have been a great Jedi Knight, and they let you go! They never appreciated you!
It was true, wasn't it? Ferus saw himself as a Padawan, standing before the Masters. Taking responsibility for something that wasn't his fault. Tru's lightsaber. He had fixed it secretly. . . .
He remembered that day. He remembered the compassion in that room.
Another vision came to him, of himself as a Padawan, accepting responsibility for what he had done. The Jedi Masters sorrowful, showing him the two paths he could take. He could have stayed. He chose to go.
His choice.
The room returned to its ruined state. He was crouching, breathing hard.
Connect.
The Force was still here in the ancient stones.
The stories of all the Jedi who had lived and died here, they were here, too. His story was here. Not as distinguished as most, shorter than many, but his. He had followed the path for as long as he could, as well as he could, and the Masters had never asked for more than that.
He felt the wisdom of the Masters inside him, and he gripped that feeling with his hands and let it fill his heart. He rose. He had no doubt that they had reached out and touched him. Many hands on his shoulder, showing him. Here is one way. Here is another. Choose.
He had come so close.
He walked out of the dark side and into the light.
I am a Jedi.
Now he knew with absolute certainty that he had to be rid of the Sith Holocron. It had been slowly poisoning him. He had been a fool to think he could take what he wanted and not be corrupted. He had fallen into the Emperor's trap. Almost.
He Force-leaped over Vader, surprising him, and let himself fall into the hole in the floor. He heard Vader's chuckle.
"Run like the coward you are!"
The wind whistled past his ears as he fell. He landed safely in the Map Room. He headed for the stairs.
He took each turning at top speed, Force-leaping most of the way. He knew where to go. The heart of the building, the power core. No longer operational, it would still contain enough residual energy, if not to destroy the Sith Holocron, then to damage it. He ran through the hallways and found the central conduit that ran, he knew, straight down to the power core. He reached into his tunic.
You are throwing away your only chance at success.
This is not the kind of success I want.
The voices of darkness were a clamor inside him as he held the Sith Holocron. He threw it in. He felt something rip inside him. It was an agonizing pain that sent him down on his knees. He breathed through it, calling on the Force to help him.
He felt it lift. He was exhausted, but he was free. He was himself again.
Vader came out of nowhere, raising a gloved hand. Ferus felt himself lifted up, over Vader's head. He couldn't breathe.
"You should know before you die that your dream is dead," Vader said. "Don't you know I can bow anyone to my will?"
Ferus was slammed against the wall. He felt himself losing consciousness.
He was glad, in the end, that he would die here at the Temple. With the ghosts of his friends, his mentors, his fellow Jedi. He would become one with the Force in the place he first discovered and nourished it.
That’s one way things could happen. Another is what happened during The Force Unleashed (which is far closer to the mature Vader I am debating with) where Vader’s attacks “redouble” and he becomes infinitely more deadly. Wouldn’t it be equally likely things played out as they did on the Invisible Hand but this time Dooku’s taunt backfired causing Vader to get mad and simply overpower him?
IG wrote:You claimed in your first post that Dooku has terrible stamina, one of the most incorrect claims you’ve made through this SS.
Dynasty of Evil wrote:
Lightsaber battles were brutal in their intensity; few duels lasted more than a minute. Even for a trained Jedi, the effort of all-out combat was exhausting: particularly when using the acrobatic maneuvers of Ataru.
Zannah claims that most duels end before a minute, and that “few duels lasted more”. “All-out combat was exhausting”, and Dooku engages in all-out combat with extremely powerful foes quite often. If you count the fight beginning as of the lightning exchange, Dooku fights Yoda (while exhausted) for a total of 80 seconds, whereas if you count the fight as only saber combat, it’s a 40 second long fight. Considering Dooku’s already tired and he’s capable of tiring Yoda in either an extremely long fight or an above average fight, I doubt this can be used to claim Dooku has bad stamina. Dooku duels Anakin and Obi-Wan together for a period of 40 seconds and then holds up against Zonakin for roughly the same amount of time. He duels two opponents that are extremely powerful individually, but together are a nigh-unstoppable duo for above average periods of time, then duels a Yoda+ opponent on his own for an above-average period of time. There’s no evidence for Dooku’s stamina really being that bad when he can contend with a duo of a character far inferior and reasonably superior, as well as an individual character marginally superior for above-average portions of time, leaving them exhausted as well.
Okay, ironically enough you validate my points about Yoda here with Zannah’s quote describing how exhaustive Ataru is. Then you go on to push for this parity to Yoda during the duel which you have yet to describe as anything more than being pushed back for 40 seconds. Again you argue that Anakin is a “Yoda+” to which I raise you the numerous quotes I posted last time claiming Yoda was stronger in the force. To top it off you completely ignored my argument about Dooku getting tired. I don’t care if Anakin had “flashes of brilliance” when we know it was “easy” for Dooku to dismantle both Kenobi and Anakin individually.
This weakness would only get worse by Revenge of the Sith as Dooku notes his body has further physically deteriorated by the time he’s onboard the Invisible Hand:
Revenge of the Sith wrote:Again, Dooku sighed. Today he felt every hour of his eighty-three years. "It is ... fatiguing, to play the villain for so long, Master. I find myself looking forward to an honorable captivity."
A captivity that would allow him to sit out the rest of the war in comfort; a captivity that would allow him to forswear his former allegiances
Dooku doesn’t have the stamina to keep up with Anakin’s blows spending “lavishly his every reserve” just to survive. So, while you can argue all day long about Dooku’s stamina with Yoda, how exhausted he was, Anakin who is not as physically dominating as Vader was already “aging him with every blow.”
Conclusion
IG wrote:Every point I’ve made still stands here. Dooku is far more powerful that ROTS Kenobi, who’s superior to his ANH iteration, who’s >= ESB Luke.
You literally conceded your entire “definition of sport argument” how does every point still stand? How is ESB Luke inferior to Ben when the very nature of your argument is that Augmentation = Power in the force? George Lucas himself has stated that the lightsaber fighting kept improving in every film, and you clearly subscribe to those statements. This is more than a double standard, it’s as you so freely call my arguments: “insane”
IG wrote:Vader has power on par with likely his AOTC iteration, somebody that Dooku is far more powerful than.
As long as the quote has any alternative interpretation, as I have shown it does, you cannot prove that.
IG wrote:Dooku’s lightning is at a similar range of power to that of Galen Marek, evident from Dooku’s capability of pressing Yoda with it.
The nature of force lightning is the reason that Yoda had difficulty with it, you established no direct link to Galen Marek, this does not work.
IG wrote:Vader’s weakness to Dun Moch in a fight is something that will haunt him against Dooku
Or just piss him off further making him more powerful and aggressive.
IG wrote:and Dooku’s stamina is top-notch.
Not against people with Anakin+ tier strength.
IG wrote:None of your points stand really, however. ESB Luke (by extension Vader) are not superior to ROTS Kenobi in any way, shape, or form.
All I was trying to explain was that the gap between them wasn’t that large and that Vader’s growth combined with Luke’s superiority to Ben who has power in the same realm as his ROTS self, perhaps even on par with his IH Kenobi self, means that Vader can compete.
IG wrote:Dooku is far above ROTS Kenobi
Based on Kenobi’s “instantaneous reactions?” Is this a joke? You haven’t substantiated one claim I made about this, the baseline being that Dooku cannot effortlessly handwave Kenobi away with a ragdoll nor can he engineer a situation that allows him to do so. It was a conscious decision for Kenobi not to erect his barrier and a tactical failure, but it was not a showing of superior power.
IG wrote:Dooku’s advantages are far greater than the limited advantages Vader possesses.
Let’s weigh the two shall we?
They both have power to suggest neither can ragdoll the other.
For team Tyranus we have:
- Superior technical skill
- Superior average speed
- A wider breadth of abilities to draw from
For Team Vader we have
- Superior stamina
- Superior Durability (which mitigates the speed advantage)
- Superior strength
- Specific resistance to lightning
You can clearly see that one set of advantages cancels out the other. It’s like the ROTS Novel says:
Revenge of the Sith wrote:Dooku's decades of combat experience are irrelevant. His mastery of swordplay is useless. His vast wealth, his political influence, impeccable breeding, immaculate manners, exquisite taste-the pursuits and points of pride to which he has devoted so much of his time and attention over the long, long years of his life-are now chains hung upon his spirit, bending his neck before the ax.
Even his knowledge of the Force has become a joke.
 The Fallen WarriorLevel Four
The Fallen WarriorLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:21 pm
 Nute_ChethrayModerator
Nute_ChethrayModerator
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:23 pm
Good post 

 The lord of hungerLevel Two
The lord of hungerLevel Two
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:37 pm
dooku s fucked 
marvelous post ISV

marvelous post ISV
 HellfireUnitLevel Six
HellfireUnitLevel Six
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:40 pm
Bad post, voting for IG.
 The lord of hungerLevel Two
The lord of hungerLevel Two
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 12:44 pm
imaoKelDorianUnit wrote:Bad post, voting for IG.
 BreakofDawnLevel Seven
BreakofDawnLevel Seven
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 3:18 pm
Wow.
 IGLevel Four
IGLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 4:09 pm
Section I - ISV’s Capabilities (or Lack Thereof)
Which is disingenuous. You’ve claimed in a previous post that Vader’s annual growth rate is a single ragdoll gap. If you cannot remember your own arguments, then perhaps calling me out on a bout of forgetfulness is rather foolish, isn’t it?
Because Vader’s improvements when he has a much, much larger amount to grow aren’t representative of his improvements with a much lesser amount to grow. For a more specific example, Luke has far more growth from (for example) ROTJ to DE than he does DN to LOTF.
Except I’m not appealing to incredulity. I’m clearly stating (and I’ve given another example above) that Vader’s growth is less when he has more room to grow than when he has less. Vader training the inquisitorius doesn’t mean that he grows there, there’s nothing that says this, nor claims it in any sense. Training someone doesn’t mean you’re growing. Vader fighting down fodder is furthermore not a showing of growth.
Dooku’s challenges are far greater than Vader’s, however. Where Vader fights relative fodder like An’ya Kuro (more on that later), Ferus Olin, and others, Dooku’s fights are against top-notch fighters like Yoda, Anakin, and Obi-Wan.
About Korriban, on Korriban, Dooku ragdolls Anakin, who’s beyond Kenobi at this point:
Yet Kenobi notes that on Geonosis, Dooku’s destruction of him was the most overpowering effect he’d ever felt:
Meaning Geonosis Dooku > Korriban Dooku, and since Dooku grows significantly across the war, it’s reasonable to claim that he could accomplish such a feat at the end of the war.
Except this kind of idea is prominently shown everywhere throughout the lore. The HoT grows far more from Act 2 to 3 than from 1 to 2. My ideas still stand here. The examples may not have been the best ones, but the argument itself stands; growth is never linear.
Per Lucas, Anakin has a greater potential, thus his own growth must be greater. It’s furthermore reasonable to claim Anakin’s superiority to ESB Luke based on the timeframe he has, with Luke’s 7 months of training to Anakin’s ten years. Two characters with similar potentials, having started from similar places, but one has 10 years to grow and the other has 7 months. Anakin’s growth is indubitably greater. In fact, the idea that Luke is subpar compared to PT Jedi is claimed by Lucas himself, as I’ve cited in a previous post:
Until the Prequels, the only Jedi we’d seen in combat were old men and an inexperienced youth… and clearly, we hadn’t seen anything.
This quote clearly outlines one major idea, that Luke Skywalker in the original trilogy is not as good of a fighter as a PT Jedi. For argument’s sake let’s say this doesn’t apply to TPM Kenobi, it still does to Jinn. And this quote is (evidently) from after all the originals were released, meaning that this applies to Luke as of ROTJ. Per Fightsaber, Luke is “a match for Darth Vader” during their fight in ROTJ. This is now indisputable fact, Darth Vader’s equal in Luke Skywalker is a worse combatant than Qui-Gon Jinn. Per Kenobi, in AOTC, Dooku’s domination of him was the greatest domination he had ever had. He claimed it was worse than even against TPM Maul. Dooku’s easy domination of Anakin during a flash of brilliance (where he’s able to channel raw power comparable to Yoda)

Anakin in one of these flashes of brilliance is able to stop a theta storm:

This provides Dooku an extremely impressive line of scaling.
We see how far beyond his apprentice Dooku is because of Kenobi during TCW S1, not long after AOTC, where Plo Koon says “you exceed your master’s skill with a blade” (referring to combatative viability, not just technical skill). So ROTS Dooku > AOTC Dooku >>> FlashofBrilliance!Anakin >>> AOTC Anakin > AOTC Kenobi ~ Jinn > ROTJ Luke ~ Vader.
So Dooku’s superiority still stands here.
See above.
And I’ve furthermore substantiated above why this is irrelevant. Dooku is superior to ROTJ Luke and Vader by a considerable margin.
Letting someone win clearly means that you’re not trying to win. You either try to win or you don’t, it’s simple. If you allow somebody else to beat you, you’re not trying to win. Chee implies this by putting the word “won” in quotes.
Which is not the point, and is completely irrelevant. Chee is responding to somebody asking about what Lucas’ 6, 4, 2 quote means, meaning that he’s referring to a quote explicitly legends. Thus it refers to legends.
Citation needed.
Sidious is incapable of ragdolling Dooku’s inferior in Maul. Thus he isn’t capable of ragdolling Dooku. Simple.
Insane because of the amounts of bullshit and contradictions to the lore in them. Your entire rebuttal to why Dooku cannot be near Yoda and Sidious consists of Gillard’s tiering system, except there’s one massive, gaping flaw. The gaps are described as massive, yet massive is subjective. There’s no validity in claiming a so called “enormous” gap is quantifiable, because enormous could mean just .1%, depending on the quantity.
There’s literally nothing that substantiates the notion that Kenobi grows on Mustafar. Kenobi’s realization stops him from holding back, but nothing in regards to gaining strength. Furthermore, per the Gillardian scale you yourself use, Kenobi is an 8, there’s no provision for him jumping to a 9 at the end of the movie, something like that would be significant and surely noted. Thus the idea that Vader is mentally hindered on Mustafar and it’s difficult for him to channel the force. This is supported by Vader himself:
He’s still conflicted on Mustafar, and emotional shock is noted to hinder a Jedi’s connection to the force by Luke Skywalker during Legacy of the Force. Vader’s surely emotionally shocked and betrayed by Padme’s (perceived) betrayal and having to fight someone that’s like a brother to him. Vader’s conflict and unstable mental state (noted by Gillard saying he’s not mastered the mental side of fighting) is evident of his inability to channel the force as well as he should, his immense raw power notwithstanding. Simply put, Anakin possesses raw power in excess of the PT Titans, but he’s too conflicted and stupid to channel it to full potency.
No, Ben’s just weaker. Like, Lucas explicitly states that we’ve not seen anything, and Kenobi is one of his examples. Given Ben is downscaled ala TPM Kenobi, who’s so much weaker than his ROTS iteration, we know that Ben being ~ IH Kenobi is incorrect.
Vader says “your powers are weak”, he’s clearly saying his powers have diminished lol.
Section II - Dooku Does Indeed, Ragdoll
You’ve clearly not read the text nor my arguments. The section I’ve cited as the “ragdoll” is not the section in the JN where Dooku chokes Kenobi out and flings him away. Dooku explicitly in the film telekinetically removes Kenobi from combat twice, once after the scene cuts to Palpatine, and next after Kenobi charges up the stairs and takes out the Super Battle Droids. This is the scene I’m referring to:
[url=https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku tk time.gif]https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku%20tk%20time.gif[/url]
Occasional clumsiness sure, but the quote means he lacks the technical skill of a lifelong master (like Dooku). His cybernetics and clumsiness to contribute to this though, yes.
Yeah, Vader’s suit is bulky and heavy, this results in Dooku gaining a vast mobility advantage too though.
Been around them sure. But does he know how they fight in all-out combat? I mean knowing how good someone in a spar is =/= knowing how good of an all out combatant they are.
Well that’s certainly the implication in your arguments. Perhaps being able to articulate better would be helpful, though I’m sure you’re trying your best. Dooku didn’t exhibit a simple “burst of speed”, as you put it. There’s not real substantiation for that. There’s furthermore no substantiation for Kenobi being caught off-guard. Let’s put this notion to rest once and for all here, shall we?
This is the “ragdoll” I’m arguing:
This, is the one you’re arguing:
This, is the one I’m arguing:
[url=https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku tk time.gif]https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku%20tk%20time.gif[/url]
This, is the one you’re arguing:
https://comicvine1.cbsistatic.com/uploads/original/12/124590/5493517-8429761051-giphy.gif
Please, before you refute a post, try reading it in its entirety first, instead of asking others to do the same, perhaps?
Except Kenobi was not caught off guard. There is absolutely no evidence that Kenobi was caught off guard. We’re referring to two completely different incidents within the text.
Except that is not what I’m referring to. I am explicitly referring to the scene where Dooku pushes Kenobi away with a “whipcrack” of power. I am not referring to the scene where Dooku kicks Kenobi. Thus Dooku is dealing with Anakin.
Yeah, and that’s because of Dooku’s skill as a fighter, not because of the duo’s deficiency as fighters. Your rebuttal does not refute my argument, it’s trying to cop out of it because you know that you’re incorrect.
Except for when he, you know, ragdolls Kenobi.
Dooku literally doesn’t get a chance to regain his composure and rethink. Kenobi is “all over him” because he’s caught completely off-guard by Kenobi’s abrupt switch from Shii-Cho and Ataru to Soresu. You’ve not cited Dooku getting a chance to regain his composure either way here. In YDR, Yoda fights Dooku and Dooku gives way “slowly, slowly” while taunting Yoda every strike. Months before ROTS, Dooku easily stops Mace’s attempts to decapitate him and mocks it to his face. But Kenobi is somehow capable of stonewalling and blitzing Dooku when he has his composure. Mace and Yoda are both canonically superior to Obi-Wan, so Dooku being caught off guard is not only supported by the novel, it’s supported by common sense.
Subjectivity of gaps, plus there’s no precedent for Mace growing drastically. Unless you’re able to prove he has mega-growth, Mace being at that level then still stands. Passive growth over time isn’t really significant either, unless the time amounts to decades.
Refer to my passive growth rebuttal, plus there’s no precedent for hindrance.
Imagine being ISV, and applying these kinds of double standards.
Or we could apply the logical conclusion, and say that Yoda’s taunting him. We know that Dooku is “an even greater lord of the Sith” compared to his Jedi self, and Dooku isn’t going to conceal power against a foe that’s a tier 9. The simplest solution is often the most accurate, and it’s simplest to claim Dooku is able to stalemate Yoda, not adhere to some convoluted conjecture you come up with.
Yoda overextending himself is proof of Dooku’s ability to contend with a combatant at a tier 9 level. Yoda’s overextension is his own fault and is no tactical failure. Dooku didn’t use underhanded trickery to make Yoda overextend himself, he’s evidently a great enough threat that it merits Yoda’s overextension, something Dooku is able to easily take advantage of. Passive growth across a year isn’t making up the gap from weak to with ROTS Sidious, and you’ve not substantiated that it should. Subjectivity also plays a role here, and “enormous” can mean even .1% when referring to vast quantities, and Yoda and Dooku’s power is vast.
No, that’s not what I was saying. I was saying Dooku’s intelligence and power (which is extremely close to Yoda and co) is what allows him to compete with the Titans. Dooku’s power greatly exceeds Vader’s, so it’s incorrect to claim that Vader has a raw power advantage, and it’s furthermore incorrect to claim that Dooku’s ability to nigh-stalemate Yoda is a result of a purely stylistic advantage, and not one of comparable raw power.

Yes, the same Kuro gets easily obliterated by Padawan Hett, very good. Though this point itself is irrelevant because of Dooku’s scaling above Vader anyway, so not the point.
Lucas quotes disagree, as I’ve proven.
Wrong occasion, and it’s only evidence of Dooku being good at exploiting openings in his opponent’s defense as he did Kenobi, Anakin, and Yoda.
There’s no confirmed mega-growth. You don’t just go from getting easily obliterated by someone to being relative to them with passive growth. Dooku being able to easily take it Kenobi while also fighting Anakin is evidence of Dooku’s superiority nonetheless.
Yes, it does denote greater power. Dooku’s augmentative strength is great enough that he’s able to hold Kenobi off while also utilizing the force to chuck stuff at Anakin. You’ve provided no evidence for why Dooku should have an advantage in leverage and positioning, so my point stands.
Refer to above, where I said that this isn’t what I’m referring to.
Dooku pushing a combat ready Kenobi away is something that’s in no way similar to the scan you’ve just shown, sans context. Here’s the full scan, for reference:

Here it’s depicted that as Dooku knocks Kenobi away, Anakin pushes him. This is a stark contrast to Dooku fighting Kenobi and Anakin and pushing a non-surprised, combat ready Kenobi. You’ve numerous times mocked and berated me for using Kenobi being surprised (though that’s not what I used), yet you purposely mislead people reading this SS in order to make me look stupid. Seems kind of hypocritical and idiotic to me.
Read my arguments above for why the ragdoll gap exists, because Kenobi isn’t surprised at all in the fight. Either Dooku is just so much faster than Kenobi that he can throw him away before Kenobi can react, or Dooku can burst through his barrier. One of those is true, and both of them denote an enormous disparity. Before calling someone out for hypocrisy, you may want to read their arguments and look at yourself first.
Read above for rebuttal.
Because there’s no surprise on Kenobi’s part. Read my arguments first, then respond.
Not what happened, read arguments before your feeble attempts to “debunk” them.
Not using a double standard here though. I’m saying that Mace can’t get a feel for Dooku’s strength through their fight, but I’m not claiming that the duo’s brief fight is a representation of how an extended duel would go, just that Dooku is not taken out by such attacks, and he’s also capable of not being taken out by Yoda’s attacks. Compare that to Kenobi being able to stonewall a surprised, caught off guard Dooku, and it’s pretty obvious Dooku isn’t near Kenobi. Your double standards are never ending, as you use Dooku being caught off-guard as a means to draw parity.
I never said that… Read my arguments first next time. Kenobi wasn’t caught off guard, stop repeating the same nonsense that makes no sense.
KENOBI WAS NOT CAUGHT OFF GUARD!
Why are you arguing this? Dooku’s attack on Kenobi is completely separate from the instance where Kenobi is caught off guard. Quit arguing nonsense and read my post first.
No, it really doesn’t. Kenobi letting go doesn’t give him more power. Anakin giving into his rage (which is when he starts hammering Dooku, after Dooku “whipcrack” blasts Kenobi) is a tier 9, backed by Gillard. Dooku loses to Zonakin, Kenobi basically gives ground constantly and has a massive advantage from teaching Anakin and knowing his style in-and-out against a hindered Anakin.
There is no difference in augmentation and raw force power. Augmentation is an expression of raw power, just like Telekinesis, Telepathy, Lightning, and many other abilities are. Kenobi doesn’t grow throughout ROTS, so you need to prove that Kenobi grows, as his realization doesn’t prove growth.
Vader moving X-Wings is nothing compared to Dooku casually ragdolling Cruisers that are hundreds of meters long. This is, after all, irrelevant as Dooku scales directly far above Vader, however.
Nah, I just realized that Dooku on Geonosis > Korriban Dooku.
What? Are you even serious right now? Yoda uses the cane in ROTS too, are you claiming in ROTS, Yoda is only capable of walking with a cane? The facts on their own stand, and your baseless claims mean nothing without substantiation, which you’ve not provided. An exhausted Dooku manages to exhaust Yoda in a duel longer than most duels. Your point that Dooku has bad stamina just doesn’t exist. I’ve given you a source, and you’ve given me jackshit as a rebuttal.
That’s not what I was saying… The quote evidently is referring to unaugmented strength, because if augmentation was included, then it would contradict G-Canon, and therefore be thrown out.
Luke matches Vader in bladelock in Return of the Jedi, a G-Canon source:

Matching somebody in bladelock is an immediate showing of parity, as your augmentation matches theirs. Luke’s physical strength + aug is at least <= Vader’s physical strength + aug. Yet despite this, per G-Canon, ROTJ Luke’s combatative potency is less than that of Jinn, who in turn scales far, far below Dooku.
I used the Mace fight to prove that Windu wasn’t too fast for Dooku, something that is clearly implied in the Kenobi comparison.
Aug matters, you know. Either way, I’ve substantiated this here, so it’s irrelevant.
The AOTC Anakin quote still stands.
So then what is the problem? I agree that the boost is not representative of his average growth, it was the fact that he went from not being able to walk to outright stomping 5 Jedi and dueling even with a Council master in a very short period of time that impressed me. Like, the boost was just the icing on the cake powerwise, I feel you misinterpreted what I meant.
Which is disingenuous. You’ve claimed in a previous post that Vader’s annual growth rate is a single ragdoll gap. If you cannot remember your own arguments, then perhaps calling me out on a bout of forgetfulness is rather foolish, isn’t it?
What? Why wouldn’t going from being unable to walk to being a council master tier in a short span of time be indicative of the kind of growth and improvements he would achieve without those hindrances? I provide more evidence with the Sa Cuis example that the growth continued and again as we see in your next statement…
Because Vader’s improvements when he has a much, much larger amount to grow aren’t representative of his improvements with a much lesser amount to grow. For a more specific example, Luke has far more growth from (for example) ROTJ to DE than he does DN to LOTF.
The best you can do to counter my argument is once again appeal to the argument of incredulity. I will remind you that saying my idea is crazy, without countering it with evidence is fallacious. You do attempt to provide a measure of evidence by citing the example of Yoda not being able to lift 5 Muntuur stones and only lifting 4 by the time of TPM. Yet, as you referenced in your previous post, conflict makes force users grow, and Yoda is more powerful by quite a margin by Revenge of the Sith judging by his encounters with Dooku and SIdious respectively (more on this later). So what you are saying is stagnation kills growth, but Vader is certainly not stagnant during this time. Vader is personally responsible for the training of the Darkside Adepts of the Empire, this includes the inquisitorious who as noted by Antennis Tremayne and seen in the Hyperspace Web Strip Evasive Action Vader hand trains. Vader has his apprentice Galen Marek to train so that he can overthrow the Emperor at this time. Vader has systems to put down and keep in service of the empire and organizations to quell into submission a matter he personally attends to:
Except I’m not appealing to incredulity. I’m clearly stating (and I’ve given another example above) that Vader’s growth is less when he has more room to grow than when he has less. Vader training the inquisitorius doesn’t mean that he grows there, there’s nothing that says this, nor claims it in any sense. Training someone doesn’t mean you’re growing. Vader fighting down fodder is furthermore not a showing of growth.
Lastly, as you know Vader also takes a personal interest in hunting Jedi survivors of Order 66. In comparison, Dooku engages in very few lightsaber duels throughout his 3 year war, Dooku spends most of his time in politics and away from the battlefield yet has a massive growth enough to compensate for the nexus of Korriban? You calling my argument “crazy” has a whole new level of irony doesn’t it? Yet I would like to run with your logic for a minute. It’s clear that Tyranus’s training of his little cadre of adepts and few lightsaber duels affords him a gargantuan amount of power growth, so then we must also concede that Vader’s training of the inquisitors, Galen Marek, and numerous battlefield and dueling scenarios affords him the same type of growth. In other words: even if we go by IG logic your arguments only serve to validate mine.
Dooku’s challenges are far greater than Vader’s, however. Where Vader fights relative fodder like An’ya Kuro (more on that later), Ferus Olin, and others, Dooku’s fights are against top-notch fighters like Yoda, Anakin, and Obi-Wan.
About Korriban, on Korriban, Dooku ragdolls Anakin, who’s beyond Kenobi at this point:
Jedi Quest: The Final Showdown wrote:Anakin was moving quickly, hugging the wall of the hangar. His focus was so intent that he did not sense Obi-Wan behind him. Obi-Wan noted this with alarm. How many times had he warned Anakin to never focus on the goal ahead only, but to cast his attention like a net, as far around him as he could? He should have sensed his Master. Obi-Wan quickened his pace. He felt the dark side of the Force grow and gather, and he wanted to call out to Anakin, but didn't want to give away their positions.
He needn't have worried. Whoever the Sith was, he knew exactly where Anakin was, for, to Obi-Wan's horror, his apprentice was suddenly lifted like a doll and flung into the air. Anakin's body slammed into the wreck of a cruiser. He fell to the ground.
Yet Kenobi notes that on Geonosis, Dooku’s destruction of him was the most overpowering effect he’d ever felt:
Legacy of the Jedi wrote:Count Dooku's fall has troubled us all," Obi-Wan acknowledged. "Now we have a great and powerful enemy." His thoughts turned to his battle with Dooku. He had never met such power in battle before. He had never come up against something that had completely overpowered him. Even meeting the Sith Lord who had killed Qui-Gon had not been the same.
Meaning Geonosis Dooku > Korriban Dooku, and since Dooku grows significantly across the war, it’s reasonable to claim that he could accomplish such a feat at the end of the war.
Again you misinterpreted what I was saying. I wasn’t implying you compared the two, I was saying you used two prodigies to try and explain away inconsistencies in growth, which doesn’t work at all. The entire example in itself is easily summarized by your own argument too. Anakin in the temple training with everyone else his skills are being somewhat dormant and thus he doesn’t grow that much in the interim, yet during wartime he blossoms into someone far more powerful. The same would go for Kenobi. So there is your explanation for why they are “inconsistent” in growth. They are constantly fighting and grow more as a result of that. This is your argument for Dooku too… if war increases the speed of growth then you have inadvertently poisoned this comparison above with hypocrisy. As for Sidious, he is yet another prodigy so it’s improbable to use him as a benchmark comparison to Vader, but even in this case he’s been draining the lifeforce of Byss and studying dark lore for years, on-top of having a newer and younger body to better sustain that power. He too has an explanation, it appears you merely have to read the source material to find it.
Except this kind of idea is prominently shown everywhere throughout the lore. The HoT grows far more from Act 2 to 3 than from 1 to 2. My ideas still stand here. The examples may not have been the best ones, but the argument itself stands; growth is never linear.
A greater prodigy you say? Please substantiate that. Anyway, I’m glad you brought up this comparison of training because it is indeed interesting. Luke doesn’t have the formal training, no. Luke is training on a backwater world with snakes and beasts of all sizes, but Luke is also being hand trained by Yoda. Anakin is sitting in a temple, occasionally going on field missions and sparring, but he has yet to face real conflict and he’s clearly not being trained in a very harsh environment by a very harsh teacher. Contrast that to Yoda who is “pushing Luke to his limits” everyday and you should be able to see why someone with Luke’s situation might be more combatively viable than Anakin.
Per Lucas, Anakin has a greater potential, thus his own growth must be greater. It’s furthermore reasonable to claim Anakin’s superiority to ESB Luke based on the timeframe he has, with Luke’s 7 months of training to Anakin’s ten years. Two characters with similar potentials, having started from similar places, but one has 10 years to grow and the other has 7 months. Anakin’s growth is indubitably greater. In fact, the idea that Luke is subpar compared to PT Jedi is claimed by Lucas himself, as I’ve cited in a previous post:
Until the Prequels, the only Jedi we’d seen in combat were old men and an inexperienced youth… and clearly, we hadn’t seen anything.
This quote clearly outlines one major idea, that Luke Skywalker in the original trilogy is not as good of a fighter as a PT Jedi. For argument’s sake let’s say this doesn’t apply to TPM Kenobi, it still does to Jinn. And this quote is (evidently) from after all the originals were released, meaning that this applies to Luke as of ROTJ. Per Fightsaber, Luke is “a match for Darth Vader” during their fight in ROTJ. This is now indisputable fact, Darth Vader’s equal in Luke Skywalker is a worse combatant than Qui-Gon Jinn. Per Kenobi, in AOTC, Dooku’s domination of him was the greatest domination he had ever had. He claimed it was worse than even against TPM Maul. Dooku’s easy domination of Anakin during a flash of brilliance (where he’s able to channel raw power comparable to Yoda)
Anakin in one of these flashes of brilliance is able to stop a theta storm:
This provides Dooku an extremely impressive line of scaling.
We see how far beyond his apprentice Dooku is because of Kenobi during TCW S1, not long after AOTC, where Plo Koon says “you exceed your master’s skill with a blade” (referring to combatative viability, not just technical skill). So ROTS Dooku > AOTC Dooku >>> FlashofBrilliance!Anakin >>> AOTC Anakin > AOTC Kenobi ~ Jinn > ROTJ Luke ~ Vader.
So Dooku’s superiority still stands here.
He does?
See above.
Are you serious? The quote you posted just says that he wasn’t trained like a PT jedi, he wasn’t, he was trained out in the wilderness by Yoda. The quote does imply some contextual relevance to Luke’s skill, but I never argued that Luke had more sophisticated technical skill, only that he was better combatively. Also, this quote says Lucas “kept improving the sword fighting” so are you conceding that ESB Luke is a better duelist than Ben too?
And I’ve furthermore substantiated above why this is irrelevant. Dooku is superior to ROTJ Luke and Vader by a considerable margin.
Woah, what do you mean by throwing the fight? Are you saying he wasn’t giving his all? The DK quote merely says Kenobi let Vader win, but it doesn’t say he didn’t try to fight. You can clearly see in the film and every other source where Kenobi “gives up” which is when he raises his lightsaber and allows Vader to strike him down.
Letting someone win clearly means that you’re not trying to win. You either try to win or you don’t, it’s simple. If you allow somebody else to beat you, you’re not trying to win. Chee implies this by putting the word “won” in quotes.
That doesn’t answer my question at all. Chee is responding to something in 2019, unless he explicitly said it goes for Legends he is referring to Canon. You really need to prove this refers to legends or it can actually be thrown out. Either way, I am beginning to fear you never read my first post, because all these arguments about Vader being equal to Ben during the fight actually mean nothing considering I posted three quotes and a passage saying after Vader killed Ben he got a type of boost and became better in all areas. This entire debate on Ben Kenobi has been pointless, but I’ll humor you:
Which is not the point, and is completely irrelevant. Chee is responding to somebody asking about what Lucas’ 6, 4, 2 quote means, meaning that he’s referring to a quote explicitly legends. Thus it refers to legends.
Yoda is hindered in that fight.
Citation needed.
He’s not, I never said or implied he was. For some bold reason you have decided to say that Sidious and Yoda are incapable of ragdolling Obi-wan and Dooku and that I challenge you: prove it.
Sidious is incapable of ragdolling Dooku’s inferior in Maul. Thus he isn’t capable of ragdolling Dooku. Simple.
Not at all what I said, you just shoved a whole paragraph of fabricated sentences in my mouth but okay. Either or, you appeal once more to that argument of incredulity which leads me to conclude you are incapable of countering my arguments without merely chastising them for their supposed “absurdity.”
Insane because of the amounts of bullshit and contradictions to the lore in them. Your entire rebuttal to why Dooku cannot be near Yoda and Sidious consists of Gillard’s tiering system, except there’s one massive, gaping flaw. The gaps are described as massive, yet massive is subjective. There’s no validity in claiming a so called “enormous” gap is quantifiable, because enormous could mean just .1%, depending on the quantity.
Yes it says he’s slower than the “duelist he once was” which refers to his state at the end of Revenge of the Sith, this doesn’t at all place him below IH Kenobi or any Kenobi before his realization.
There’s literally nothing that substantiates the notion that Kenobi grows on Mustafar. Kenobi’s realization stops him from holding back, but nothing in regards to gaining strength. Furthermore, per the Gillardian scale you yourself use, Kenobi is an 8, there’s no provision for him jumping to a 9 at the end of the movie, something like that would be significant and surely noted. Thus the idea that Vader is mentally hindered on Mustafar and it’s difficult for him to channel the force. This is supported by Vader himself:
Dark Lord: The Rise of Darth Vader wrote:Anakin had still been between worlds then, and vulnerable.
He’s still conflicted on Mustafar, and emotional shock is noted to hinder a Jedi’s connection to the force by Luke Skywalker during Legacy of the Force. Vader’s surely emotionally shocked and betrayed by Padme’s (perceived) betrayal and having to fight someone that’s like a brother to him. Vader’s conflict and unstable mental state (noted by Gillard saying he’s not mastered the mental side of fighting) is evident of his inability to channel the force as well as he should, his immense raw power notwithstanding. Simply put, Anakin possesses raw power in excess of the PT Titans, but he’s too conflicted and stupid to channel it to full potency.
Really? So you think that Ben having an older vessel that prevents him from dueling the way he used to means he diminished in his actual power or the power he can apply in combat?
No, Ben’s just weaker. Like, Lucas explicitly states that we’ve not seen anything, and Kenobi is one of his examples. Given Ben is downscaled ala TPM Kenobi, who’s so much weaker than his ROTS iteration, we know that Ben being ~ IH Kenobi is incorrect.
According to Vader, Kenobi’s power’s haven’t diminished at all, so the quote saying he’s slower is only saying that his applicable skill in a duel is inferior to what he could once do, not that he has lost any of his actual power. This entire argument that because Ben is about 20 years older he somehow lost his power is bogus. In the words of Han:
Vader says “your powers are weak”, he’s clearly saying his powers have diminished lol.
Section II - Dooku Does Indeed, Ragdoll
Slow down, I just explained this to you. Kenobi rushed Dooku full defenses not erected thinking his back was turned, in that second, Dooku turned around and picked him up and he couldn’t gather his energies in time due to the suddenness of the attack catching him off-guard. What part of that argument do you not understand? Kenobi’s defensive style is irrelevant if he’s not employing it at the time…
You’ve clearly not read the text nor my arguments. The section I’ve cited as the “ragdoll” is not the section in the JN where Dooku chokes Kenobi out and flings him away. Dooku explicitly in the film telekinetically removes Kenobi from combat twice, once after the scene cuts to Palpatine, and next after Kenobi charges up the stairs and takes out the Super Battle Droids. This is the scene I’m referring to:
[url=https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku tk time.gif]https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku%20tk%20time.gif[/url]
That quote doesn’t mean you think it does. Vader has cybernetic limbs and big feet, according to Galen Marek he has “an occasional clumsiness”:
Occasional clumsiness sure, but the quote means he lacks the technical skill of a lifelong master (like Dooku). His cybernetics and clumsiness to contribute to this though, yes.
Yet he’s also “sure on his feet.” This makes sense within the context of the character as the suit itself is bulky and heavy, but his “lack of polish” just means his style isn’t as pretty as Dooku’s. Vader can compensate for this in bursts as shown here:
Yeah, Vader’s suit is bulky and heavy, this results in Dooku gaining a vast mobility advantage too though.
Ferus Olin (who has been around the council masters) directly compares his skill to that of the Council Masters. The only way to reconcile that quote with this one is that it must refer to the clumsiness Vader occasionally sports which doesn’t really factor in since he can perform council level swordsmanship if he needs to anyway.
Been around them sure. But does he know how they fight in all-out combat? I mean knowing how good someone in a spar is =/= knowing how good of an all out combatant they are.
No, you just didn’t read the quote that went with my argument. I merely cited that Luke was faster than Ben and more viable, I did not argue his speed denoted greater power. Even if I were to argue that, you are making another false comparison, there is a colossal difference between being caught off guard by a burst of speed and being consistently faster than another character. Perhaps stop accusing me of double standards and start comprehending my arguments?
Well that’s certainly the implication in your arguments. Perhaps being able to articulate better would be helpful, though I’m sure you’re trying your best. Dooku didn’t exhibit a simple “burst of speed”, as you put it. There’s not real substantiation for that. There’s furthermore no substantiation for Kenobi being caught off-guard. Let’s put this notion to rest once and for all here, shall we?
This is the “ragdoll” I’m arguing:
Revenge of the Sith wrote:He gathered the Force once more in a single indrawn breath that summoned power from throughout the universe; the slightest whipcrack of that power, negligent as a flick of his wrist, sent Kenobi flying backward to crash hard against the wall, but Dooku didn't have time to enjoy it.
This, is the one you’re arguing:
Revenge of the Sith wrote:Before their pieces could even hit the floor Dooku was in motion, landing a spinning side-stamp that folded Skywalker in half; he used his last burst of dark power to continue his spin into a blindingly fast wheel-kick that brought his heel against the point of Kenobi's chin with a crack like the report of a huge-bore slugthrower, knocking the Jedi Master back down the stairs. Sounded like he'd broken his neck. Wouldn't that be lovely?
This, is the one I’m arguing:
[url=https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku tk time.gif]https://static1.comicvine.com/uploads/original/11122/111225346/5370655-dooku%20tk%20time.gif[/url]
This, is the one you’re arguing:
https://comicvine1.cbsistatic.com/uploads/original/12/124590/5493517-8429761051-giphy.gif
Please, before you refute a post, try reading it in its entirety first, instead of asking others to do the same, perhaps?
What? It changes everything if the opponent is caught off-guard, they can’t adequately defend themselves. Are you honestly the guy that thinks a sucker punch denotes greater speed? Because that’s the logic you are arguing.
Except Kenobi was not caught off guard. There is absolutely no evidence that Kenobi was caught off guard. We’re referring to two completely different incidents within the text.
Why is Anakin at all relevant in this scenario? Dooku has just in-capped Anakin with a kick and Dooku turned at the last minute to seize Kenobi. Anakin is not at all relevant to Kenobi being caught off-guard or this entire situation.
Except that is not what I’m referring to. I am explicitly referring to the scene where Dooku pushes Kenobi away with a “whipcrack” of power. I am not referring to the scene where Dooku kicks Kenobi. Thus Dooku is dealing with Anakin.
Because Dooku is literally making them trip over each other…
Yeah, and that’s because of Dooku’s skill as a fighter, not because of the duo’s deficiency as fighters. Your rebuttal does not refute my argument, it’s trying to cop out of it because you know that you’re incorrect.
Good for Dooku that he can very methodically deal with two opponents at once, forcing them in each other’s way while deftly moving out of attack vectors and keeping them on their toes. That doesn’t translate to him being a ragdoll gap ahead of Kenobi.
Except for when he, you know, ragdolls Kenobi.
Considering Dooku has an in-depth knowledge of all lightsaber forms and has a chance to regain his composure and rethink the situation, I don’t think you can actually argue that his surprise affects his combative viability at all. That’s speculation without evidence anyway.
Dooku literally doesn’t get a chance to regain his composure and rethink. Kenobi is “all over him” because he’s caught completely off-guard by Kenobi’s abrupt switch from Shii-Cho and Ataru to Soresu. You’ve not cited Dooku getting a chance to regain his composure either way here. In YDR, Yoda fights Dooku and Dooku gives way “slowly, slowly” while taunting Yoda every strike. Months before ROTS, Dooku easily stops Mace’s attempts to decapitate him and mocks it to his face. But Kenobi is somehow capable of stonewalling and blitzing Dooku when he has his composure. Mace and Yoda are both canonically superior to Obi-Wan, so Dooku being caught off guard is not only supported by the novel, it’s supported by common sense.
Again, it’s just a case of you assuming things. How powerful was Mace during this period? We really don’t know, we do know that by ROTS he’s a hair away from a 9 compared to Dooku’s 8. So there’s a fair gap between the two.
Subjectivity of gaps, plus there’s no precedent for Mace growing drastically. Unless you’re able to prove he has mega-growth, Mace being at that level then still stands. Passive growth over time isn’t really significant either, unless the time amounts to decades.
Not prime or unhindered Yoda.
Refer to my passive growth rebuttal, plus there’s no precedent for hindrance.
You mean you are actually gonna provide evidence for one of your offhanded claims?
Imagine being ISV, and applying these kinds of double standards.
Dialogue is important.
Yoda notes that Dooku is weaker than his Jedi self. This implies Dooku is concealing his power to decieve Yoda. Then:
Or we could apply the logical conclusion, and say that Yoda’s taunting him. We know that Dooku is “an even greater lord of the Sith” compared to his Jedi self, and Dooku isn’t going to conceal power against a foe that’s a tier 9. The simplest solution is often the most accurate, and it’s simplest to claim Dooku is able to stalemate Yoda, not adhere to some convoluted conjecture you come up with.
When Yoda leaps overextending himself, Dooku decided to fire a torrent of lightning at Yoda’s back which sends him flying. Also as you said, this battle takes place in 20 bby which is a good distance away from ROTS meaning it has no relevance really. Revenge of the Sith Yoda is a 9, Dooku is an 8. The gap is “enormous.” Any fights prior can’t make it any smaller.
Yoda overextending himself is proof of Dooku’s ability to contend with a combatant at a tier 9 level. Yoda’s overextension is his own fault and is no tactical failure. Dooku didn’t use underhanded trickery to make Yoda overextend himself, he’s evidently a great enough threat that it merits Yoda’s overextension, something Dooku is able to easily take advantage of. Passive growth across a year isn’t making up the gap from weak to with ROTS Sidious, and you’ve not substantiated that it should. Subjectivity also plays a role here, and “enormous” can mean even .1% when referring to vast quantities, and Yoda and Dooku’s power is vast.
If you want to argue Dooku’s style is potentially what allows him to play with the titans that’s fine. Yoda is a midget using a highly exhaustive form that requires him to cannonball across the room to strike, Dooku is a 6’5 tall man who uses a form designed to conserve energy and keep foes at arms length. So yeah, Dooku the giant can keep the midget away for a little while and still loses every time. This will certainly help him against Vader won’t it?
No, that’s not what I was saying. I was saying Dooku’s intelligence and power (which is extremely close to Yoda and co) is what allows him to compete with the Titans. Dooku’s power greatly exceeds Vader’s, so it’s incorrect to claim that Vader has a raw power advantage, and it’s furthermore incorrect to claim that Dooku’s ability to nigh-stalemate Yoda is a result of a purely stylistic advantage, and not one of comparable raw power.
This is ANH Vader, pre Ben death boost and Kuro certainly is not fodder she’s “one of the greatest Jedi”, her students are “the best in the temple” and she has the ability to phase through matter. She’s also not post prime, no idea where you got that, all the Jedi who survived Order 66 have been “honing their skills”
Yes, the same Kuro gets easily obliterated by Padawan Hett, very good. Though this point itself is irrelevant because of Dooku’s scaling above Vader anyway, so not the point.
You failed to actually make a compelling argument so you resort to holistic portrayal. Even this argument you fail, as Vader has shown no such incompetence as of his prime or even in the example you cited.
Lucas quotes disagree, as I’ve proven.
Vader won’t be thinking “oh he’s distracted, I’ll take him from behind!.”
Wrong occasion, and it’s only evidence of Dooku being good at exploiting openings in his opponent’s defense as he did Kenobi, Anakin, and Yoda.
Again that means nothing. The duel takes place before the Outer rim sieges which last five months. That means this is at LEAST five months for Kenobi to grow and become relativistic to Dooku.
There’s no confirmed mega-growth. You don’t just go from getting easily obliterated by someone to being relative to them with passive growth. Dooku being able to easily take it Kenobi while also fighting Anakin is evidence of Dooku’s superiority nonetheless.
Yes, because obviously holding someone at bay with one-hand denotes greater power and has nothing to do with leverage and positioning at all.
Yes, it does denote greater power. Dooku’s augmentative strength is great enough that he’s able to hold Kenobi off while also utilizing the force to chuck stuff at Anakin. You’ve provided no evidence for why Dooku should have an advantage in leverage and positioning, so my point stands.
The passage is referring to Dooku kicking Kenobi. If you want to draw ragdoll tier gaps off of kicking someone that doesn’t work. Darth Maul can kick Darth Sidious back at the apex of their duel. Even if you argue that gap is smaller, Sidious is still more powerful meaning that kicks during duels mean absolutely nothing.
Refer to above, where I said that this isn’t what I’m referring to.
What? Are you arguing that force pushing your opponent denotes a vast amount of superior power? Let me point you to Dooku then:
Throughout this entire debate you have repeatedly cited Dooku’s relativity to Anakin and Kenobi at the same time, insinuating you do not think Anakin is a ragdoll tier gap above Dooku. Yet we see Anakin push Dooku, which by your logic denotes a vast gap between the two. So Anakin as of the Invisible hand is more powerful than Count Dooku. Kenobi then grows to become the equal of MFV by the end of the film who is far more powerful than IH Anakin as he has “just taken force LSD” and “jumped to a nine.” Tell me how does Dooku make up for that gap?
Dooku pushing a combat ready Kenobi away is something that’s in no way similar to the scan you’ve just shown, sans context. Here’s the full scan, for reference:
Here it’s depicted that as Dooku knocks Kenobi away, Anakin pushes him. This is a stark contrast to Dooku fighting Kenobi and Anakin and pushing a non-surprised, combat ready Kenobi. You’ve numerous times mocked and berated me for using Kenobi being surprised (though that’s not what I used), yet you purposely mislead people reading this SS in order to make me look stupid. Seems kind of hypocritical and idiotic to me.
You are right there is no “ragdoll sequence” in the book. In the novelization, Dooku kicks Kenobi once and pushes Kenobi once, neither of which denote the superiority of the “ragdoll tier gap” between the two you keep arguing. Like it baffles me that you cite the “disproportionate strength of a barrier” and still consider it completely reasonable to argue that Kenobi is but a flick of the wrist away from Dooku. It’s not just baffling, it’s hypocritical.
Read my arguments above for why the ragdoll gap exists, because Kenobi isn’t surprised at all in the fight. Either Dooku is just so much faster than Kenobi that he can throw him away before Kenobi can react, or Dooku can burst through his barrier. One of those is true, and both of them denote an enormous disparity. Before calling someone out for hypocrisy, you may want to read their arguments and look at yourself first.
Once again “the attack had been too sudden” and he thought Dooku was preoccupied with Anakin, this burst of speed means nothing.
Read above for rebuttal.
Ah, so your double standards are on full display. Alright. So Krayt was "completely taken by surprise" and this differs from Kenobi how?
Because there’s no surprise on Kenobi’s part. Read my arguments first, then respond.
Compare that to Obi-wan not even being able to muster his energies because of how sudden the attack was. So yes, the burst of speed denotes that Dooku can ragdoll an off-guard Kenobi nothing more. I’m getting tired of debunking the same arguments over and over.
Not what happened, read arguments before your feeble attempts to “debunk” them.
You use Mace now but later in this very post you will argue that the duel was so brief that Mace “couldn’t get a feel” for Dooku’s strength. These double standards are just non-stop aren’t they? Anyway, the combat with Yoda means nothing unless you can disprove Kenobi’s relativity to Dooku. The argument I use in itself is evidence. The form changing is speculation and really nothing suggests that it hindered him combatively.
Not using a double standard here though. I’m saying that Mace can’t get a feel for Dooku’s strength through their fight, but I’m not claiming that the duo’s brief fight is a representation of how an extended duel would go, just that Dooku is not taken out by such attacks, and he’s also capable of not being taken out by Yoda’s attacks. Compare that to Kenobi being able to stonewall a surprised, caught off guard Dooku, and it’s pretty obvious Dooku isn’t near Kenobi. Your double standards are never ending, as you use Dooku being caught off-guard as a means to draw parity.
Now I’m more than confused, I have no idea what you are trying to do. Kenobi’s passive barrier is much weaker than his active barrier and passive barriers really mean nothing. Kenobi was caught off-guard, you used some random quote about Kenobi’s reactionary times being instantaneous to try to disprove something the junior novel makes painfully evident.
I never said that… Read my arguments first next time. Kenobi wasn’t caught off guard, stop repeating the same nonsense that makes no sense.
THE ATTACK HAD BEEN TOO SUDDEN!
Why are you arguing this? Dooku’s attack was too sudden for a Kenobi who thought that Dooku was preoccupied with Anakin, but he was wrong. Quit arguing that Kenobi’s tactical error somehow translates to a vast disparity in power, it makes you look bad.
KENOBI WAS NOT CAUGHT OFF GUARD!
Why are you arguing this? Dooku’s attack on Kenobi is completely separate from the instance where Kenobi is caught off guard. Quit arguing nonsense and read my post first.
I’ll just take a page from your book. Let’s say that Kenobi isn’t a nine, but can compete with one like MFV, that still puts him as better than Dooku, since Dooku is locked beneath IH Anakin. Again, you ignored my point about Kenobi “letting go” which gave him access to far more power.
No, it really doesn’t. Kenobi letting go doesn’t give him more power. Anakin giving into his rage (which is when he starts hammering Dooku, after Dooku “whipcrack” blasts Kenobi) is a tier 9, backed by Gillard. Dooku loses to Zonakin, Kenobi basically gives ground constantly and has a massive advantage from teaching Anakin and knowing his style in-and-out against a hindered Anakin.
There is a fundamental difference between augmentation and raw force power, especially in a vessel as old as Obi-wan. Also, being a shadow of Mustafar Kenobi that can contend with Anakin is not at all bad. Consider the kind of growth Kenobi must gain throughout Revenge of the Sith and juxtapose that with the unquantifiable deterioration he experienced. Now, try and prove that Ben who is compared to his prime self is beneath the Kenobi who was making Dooku sweat on the Hand.
There is no difference in augmentation and raw force power. Augmentation is an expression of raw power, just like Telekinesis, Telepathy, Lightning, and many other abilities are. Kenobi doesn’t grow throughout ROTS, so you need to prove that Kenobi grows, as his realization doesn’t prove growth.
You aren’t reading my quotes at all, that’s all but confirmed now.
That statement attributes Luke’s lack of confidence as the reason he can’t lift the ship, it’s asinine that you would argue this point considering, as you said earlier; Luke can tag Vader and is out of his ragdoll range. If you truly think that Luke shares some relativity with ESB Vader then you must admit that he is above ANH Vader via his comparison with Ben, who is at least more powerful than Dark Times Vader who is capable of exceeding the X-wing feat only a few months after Revenge of the Sith:
Vader moving X-Wings is nothing compared to Dooku casually ragdolling Cruisers that are hundreds of meters long. This is, after all, irrelevant as Dooku scales directly far above Vader, however.
Good on you for entirely conceding your point about the weakness of Korriban’s nexus relative to the EmpalSuRecon though. I’m impressed you can suppress your ego enough to admit you are wrong.
Nah, I just realized that Dooku on Geonosis > Korriban Dooku.
You implied that you had definitive proof that Dooku can exhaust Dooku due to his skill. Yoda “lacks the stamina of youth” and literally has arthritis and needs a cane to walk. In order to duel he uses the most physically exhausting form bar Juyo so of course after he deactivates his force reserves he will feel fatigue. This means nothing.
What? Are you even serious right now? Yoda uses the cane in ROTS too, are you claiming in ROTS, Yoda is only capable of walking with a cane? The facts on their own stand, and your baseless claims mean nothing without substantiation, which you’ve not provided. An exhausted Dooku manages to exhaust Yoda in a duel longer than most duels. Your point that Dooku has bad stamina just doesn’t exist. I’ve given you a source, and you’ve given me jackshit as a rebuttal.
You straight up ignored my entire argument. Like, I can only assume this is willful ignorance because I can’t fathom this level of stupidity. The feats of strength Vader can perform as a cyborg are far greater than that of Anakin. This is literally compared to having very little access to the temples records, to having all of it at his fingertips from across the galaxy, which denotes it’s a huge gap. His augmentation and powerlevel means jack shit when he himself says that the feats he can perform now are better.
That’s not what I was saying… The quote evidently is referring to unaugmented strength, because if augmentation was included, then it would contradict G-Canon, and therefore be thrown out.
Luke matches Vader in bladelock in Return of the Jedi, a G-Canon source:
Matching somebody in bladelock is an immediate showing of parity, as your augmentation matches theirs. Luke’s physical strength + aug is at least <= Vader’s physical strength + aug. Yet despite this, per G-Canon, ROTJ Luke’s combatative potency is less than that of Jinn, who in turn scales far, far below Dooku.
You argue this now, yet argued earlier his contention with mace was a showing placing him above the likes of Kenobi. To quote you: “Your double standards astound me.”
I used the Mace fight to prove that Windu wasn’t too fast for Dooku, something that is clearly implied in the Kenobi comparison.
You haven’t drawn any connection between Vader being physically inferior to Yoda or why.
Aug matters, you know. Either way, I’ve substantiated this here, so it’s irrelevant.
You haven’t backed anything up yet and Vader can still be stronger than AOTC Anakin by your quote, why must you chastise me for arguing something you have yet to even address?
The AOTC Anakin quote still stands.
 IGLevel Four
IGLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 4:11 pm
Section III - Dooku ~ Yoda Still Exists
Prove he can’t. Flow Walking is literally time travelling backwards except you can’t leave an impact upon it. Jacen is able to definitively claim Anakin > the rest of the Jedi, it’s not conjecture, it’s a definitive statement. He couldn’t make that statement without absolute certainty, so naturally it stands to reason that he can sense force signatures.
Potentially means possibly, not “maybe sometime in the future”, in this context. Be logical, for once. And my claim is simple, Anakin is more powerful than BoROTS Yoda, who’s a tier 9. Yoda could’ve grown across ROTS, we don’t know that he didn’t. Your entire rebuttals are built on “well maybe they grew”, so I’ll apply that same logic here. Anakin being relative to Yoda is supported by Gillard claiming he’s a nine as well.
Anakin giving into his rage is him as a 9. Dooku is capable of contending with Anakin beginning to enter his rage-mode, but only gets beaten completely by a berserk-rage Anakin. Dooku furthermore has a stylistic disadvantage because Anakin has greater mobility plus strength + raw power, advantages Vader lacks.
Do your double standards never end? Anakin doesn’t use the DS only in YDR, he’s not a full Dark Sider. Nor is Whie, and nor is Scout. You use an author quote, but then begrudge and mock me when I do. My opinion of you is dropping by the second. Yoda is capable of drawing upon the dark (as he does) without going full DS. Anakin does the same, so there’s no reason Yoda can’t.
We know Kenobi isn’t near Dooku, and we know Dooku’s performances against Yoda in other instances portray the two as close together, so there’s no real claim that they’re far apart.
Yoda doesn’t draw fully into his hate, but he does draw from the dark as well, evident by the “dark, drunken Vjun air” line. My Anakin example supports this notion as well.
Yoda loved Dooku enough to kill him, yes. Seems to me like he’s drawing upon his anger. His love for Dooku is corrupted by Vjun, turning it into something that’s making him draw on the dark in him. Yoda drawing on the dark and light in tandem isn’t the point, because Yoda doing so isn’t a hindrance. Anakin cannot use both sides in tandem either, yet he’s not “poisoned”. It’s clear Yoda isn’t hindered, as he clearly seems to be utilizing the dark within him. Dooku goading someone in a fight is something he always does. He literally goads Anakin while Anakin is using his rage.
When Yoda calms down after, that’s not him ending the duel outright. Dooku’s already tired, and it’s said, “blades flashed and and flared stutters of light, blood red and sea green”. Dooku’s exhausted and still nigh-stalemating Yoda. Before this he’s already pushed back “slowly, slowly”, so Dooku being pushed back isn’t “ending the duel outright”. Dooku isn’t superior or equal, just extremely close to Yoda. He can’t overpower a force greater than him, it’s basic physics.
Context, Context, Context
This is after Dooku activates a missile and gives Yoda an ultimatum, take out Dooku or save “Obi-Wan and your precious Skywalker and and your little Padawans”. Like, if Yoda went after Dooku that’s going pure DS, instead, Yoda is just partly DS corrupted from Vjun, but still mostly LS. That doesn’t exclude him being amped though.
Yoda being the novice does make sense to a degree, but the context isn’t purely on Vjun that the quote is referring to. Stewart prefaces with, “Yoda is always in touch with the force”, and Yoda’s greater mastery of the force is surely what makes him in expert with drawing upon the nexus of Vjun. Add to this the fact that Yoda has greater experience in general with the Force, and there’s a stronger chance that Yoda is, indeed, the “expert surfer”. Add to this the fact that Yoda’s resisting the dark to a degree, but also giving into it similar to Anakin and you arrive at a simple conclusion, Yoda is amped as well.
Yes, I know that. Yet that’s irrelevant, because when Hidalgo makes that statement, ROTS is not canon. We have to once again arrive at the simplest possible conclusion, and not a convoluted one, that Hidalgo is indeed, referring to what viewers have already seen, Attack of the Clones, and not what is being previewed and what they haven’t already seen. I’m not disputing that ROTS wasn’t nearly done being filmed, but within the Q&A reflects what the audience has seen, and not what they haven’t, thus the statement refers to AOTC Anakin. It’s also in line with Lucas’ vision that ROTJ Vader ~ ROTJ Luke < Jinn.
This reconciled with Lucas’ statement on how we hadn’t seen anything leaves us with a clear conclusion. The moment we truly do see “something” is the Duel of the Fates. When we see a “real JedI” fight a “real Sith”. This is the defining moment in combat, and it’s evident that Jinn > Luke from an intent perspective, as well as from Lucas’ comments.
Why is Kenobi’s lifespan equivalent to Dooku’s? Like, we have people with all kinds of ages in SW, and there’s a clear direct comparison + Lucas quote affirming Kenobi is way worse in the OT.
Section IV - Lightning to Tutaminis
It is with a barrier, yes. But tutaminis creates a 1:1 comparison between the two. Tutaminis is simply energy absorption, and Lightning is obviously energy. The most powerful of masters being challenged by lightning is meaningless, when we see Yoda and Sidious being evenly matched in their lightning to tutaminis clash, and OOU quotes declaring the pair equals.
Simple, Dooku’s ability to press Yoda with it is the evidence I need. I’ve literally cited a dozen instances, from C-Canon to G-Canon why Vader is immensely below Yoda. Dooku’s ability to make Yoda struggle is evident of this.
Except the gaps between Gillardian tiers are subjective. As I’ve given an example of before, .1% of an immense quantity is still “enormous”. 0.1% percent of a trillion dollars is still an immense quantity. Yoda possesses immense power, so the idea that Gillardian tiers magically mean that Yoda stomps Dooku in his prime is completely bullshit. Kenobi isn’t near Dooku, so thus your three options are rendered moot.
Yet Mustafar Kenobi ~ IH Kenobi, as that realization means shit in terms of power.
Barriers are good against TK. Not against lightning. Logically, they’re bad against them, because a barrier is a bubble of TK, whereas Tutaminis, an ability Vader has shown little proficiency in compared to Yoda creates a 1:1 comparison between the two. Given that Vader having superior physical strength is debunked already, and Dooku’s raw power is greatly in excess of Vader’s, it’s evident why Dooku wins this.
But does Starkiller use Padme, Vader’s one emotional weakness against him? Vader goes into a berserk rage when taunted about her, it’s evident that he’d go into one now as well. Dooku’s immense power advantage, tactical advantage, skill advantage, and mobility advantage are all things that will decide this fight in his favor.
Yet the point here being that Dooku’s stamina isn’t bad. Dooku as of ROTS (the iteration I’m arguing, not AOTC) is able to take on Anakin and Obi-Wan for far longer than a minute. Therefore his stamina isn’t dogshit as you’re suggesting, and Dooku’s superior strength in the force mitigates his older body. Funny you bring up Anakin, by the way, because Dooku matches the tier 9 Zonakin in bladelock for 13 seconds with a minor advantage throughout it. Then they disengage and Anakin starts obliterating.
Conclusion
Like ISV, let’s weigh the two shall we?
Dooku has such a greater power advantage that he may be able to ragdoll Vader, but otherwise:
For Team Dooku we have:
For Team Vader we have:
It’s clear that Dooku possesses far, far greater advantages than Vader does here, and that Vader doesn’t particularly stand much of a chance.
Have you even read any of my quotes? Prove he can sense force signatures during his flow-walking.
Prove he can’t. Flow Walking is literally time travelling backwards except you can’t leave an impact upon it. Jacen is able to definitively claim Anakin > the rest of the Jedi, it’s not conjecture, it’s a definitive statement. He couldn’t make that statement without absolute certainty, so naturally it stands to reason that he can sense force signatures.
He could just be saying that Anakin’s potential is greater but even if he wasn’t, possibly denotes uncertainty. I gave you many quotes saying Yoda was the most powerful Jedi as of Revenge of the Sith and you made the claim he was equal to, or more powerful than Yoda. You have failed at explaining why this is the case.
Potentially means possibly, not “maybe sometime in the future”, in this context. Be logical, for once. And my claim is simple, Anakin is more powerful than BoROTS Yoda, who’s a tier 9. Yoda could’ve grown across ROTS, we don’t know that he didn’t. Your entire rebuttals are built on “well maybe they grew”, so I’ll apply that same logic here. Anakin being relative to Yoda is supported by Gillard claiming he’s a nine as well.
Ah, so given this new evidence and my quote, we can conclude that the 9 is in reference to when he gives into the Darkside, yet he still starts the film as an 8.
Anakin giving into his rage is him as a 9. Dooku is capable of contending with Anakin beginning to enter his rage-mode, but only gets beaten completely by a berserk-rage Anakin. Dooku furthermore has a stylistic disadvantage because Anakin has greater mobility plus strength + raw power, advantages Vader lacks.
Once again:
Vjun is a Darkside nexus and those who are connected to the lightside of the force find their powers “diminished” while those who wield the dark side are “amazed at the strength they gain.” Essentially, I already proved Yoda is not full DS and Yoda actively resists the nexus earlier in the book:
Do your double standards never end? Anakin doesn’t use the DS only in YDR, he’s not a full Dark Sider. Nor is Whie, and nor is Scout. You use an author quote, but then begrudge and mock me when I do. My opinion of you is dropping by the second. Yoda is capable of drawing upon the dark (as he does) without going full DS. Anakin does the same, so there’s no reason Yoda can’t.
With all this evidence, we return the fact we know that Yoda and Dooku have an “enormous gap” by Revenge of the Sith and Dooku is relativistic to Kenobi, so it is far more likely and fits better with the lore for Yoda to be hindered while Dooku is amped. If you still aren’t convinced, Yoda and Dooku's dialogue in the duel suggests he is actively resisting the darkside:
We know Kenobi isn’t near Dooku, and we know Dooku’s performances against Yoda in other instances portray the two as close together, so there’s no real claim that they’re far apart.
Dooku is trying to goad Yoda into giving into his hate, which Yoda clearly has not done at this point in the duel, this is after the line “in the dark, drunken Vjun air, Yoda was terrible to behold.” Which means that Yoda has not given into the Darkside and by definition of being a lightsider on a “Dark Side Site” such as Vjun, Yoda would find his powers “diminished.”
Yoda doesn’t draw fully into his hate, but he does draw from the dark as well, evident by the “dark, drunken Vjun air” line. My Anakin example supports this notion as well.
The “even here on Vjun” is very important as it insinuates that the Darkside is trying to corrupt him hence the “whispering” but he chooses to “love” signifying his resistance to all those “whispers.” Here we see Yoda repel all the anger he feels, but we know he has not yet used it or Dooku wouldn’t have been goading him to give into his anger. If Yoda does give into the Darkside at some point like I said it is a hindrance because Yoda is not shown capable of using the light and dark sides in tandem and thus the two would be clashing, which ends up “poisoning” him. Notice how after he calms himself, we see Yoda immediately drive Dooku back and almost end the duel outright:
Yoda loved Dooku enough to kill him, yes. Seems to me like he’s drawing upon his anger. His love for Dooku is corrupted by Vjun, turning it into something that’s making him draw on the dark in him. Yoda drawing on the dark and light in tandem isn’t the point, because Yoda doing so isn’t a hindrance. Anakin cannot use both sides in tandem either, yet he’s not “poisoned”. It’s clear Yoda isn’t hindered, as he clearly seems to be utilizing the dark within him. Dooku goading someone in a fight is something he always does. He literally goads Anakin while Anakin is using his rage.
When Yoda calms down after, that’s not him ending the duel outright. Dooku’s already tired, and it’s said, “blades flashed and and flared stutters of light, blood red and sea green”. Dooku’s exhausted and still nigh-stalemating Yoda. Before this he’s already pushed back “slowly, slowly”, so Dooku being pushed back isn’t “ending the duel outright”. Dooku isn’t superior or equal, just extremely close to Yoda. He can’t overpower a force greater than him, it’s basic physics.
Yoda chooses not to “annihilate him utterly” and he has to resist the urge, which again means he isn’t drawing on it, the allusions to the air are of it’s corrupting nature not that he is drawing on it's power.
Context, Context, Context
This is after Dooku activates a missile and gives Yoda an ultimatum, take out Dooku or save “Obi-Wan and your precious Skywalker and and your little Padawans”. Like, if Yoda went after Dooku that’s going pure DS, instead, Yoda is just partly DS corrupted from Vjun, but still mostly LS. That doesn’t exclude him being amped though.
The quote says that Yoda “tapped in” and that one “could” use it like waves. But we must question what Stewart really meant by the “expert surfer.” Initial thoughts lead us to conclude it’s Yoda; he’s older, wiser, and more powerful. Yet the context of the quote is that it’s the expert and novice on Vjun. With this in mind, who has more experience actively weidling the darkside? Who would be the “expert” at “doing more with that (darkside)” power. Well obviously it would be Count Dooku. This makes sense in the context of the duel since the proverbial darkside “novice” (Yoda) is in a situation where it’s “easier for him to lose control.” We see several times where Yoda actively resists the temptation of the Darkside, and during a fight where one has to be focused on the opponent a distraction such as this that “diminishes” his power, would surely hinder him.
Yoda being the novice does make sense to a degree, but the context isn’t purely on Vjun that the quote is referring to. Stewart prefaces with, “Yoda is always in touch with the force”, and Yoda’s greater mastery of the force is surely what makes him in expert with drawing upon the nexus of Vjun. Add to this the fact that Yoda has greater experience in general with the Force, and there’s a stronger chance that Yoda is, indeed, the “expert surfer”. Add to this the fact that Yoda’s resisting the dark to a degree, but also giving into it similar to Anakin and you arrive at a simple conclusion, Yoda is amped as well.
Perhaps you are simply oblivious to what Insider was promoting at this time. Each issue was a “sneak peak” of what was to come in Revenge of the Sith, which is even implied in one of Hidalgo’s answers to a Q & A at this time:
Just saying it is not the equivalent of proving it. I gave you a source claiming that most of the filming was done at this time, I explained that the time period it was released in could easily be referring to Revenge of the Sith Anakin. You have just repeated the same thing without evidence.
Yes, I know that. Yet that’s irrelevant, because when Hidalgo makes that statement, ROTS is not canon. We have to once again arrive at the simplest possible conclusion, and not a convoluted one, that Hidalgo is indeed, referring to what viewers have already seen, Attack of the Clones, and not what is being previewed and what they haven’t already seen. I’m not disputing that ROTS wasn’t nearly done being filmed, but within the Q&A reflects what the audience has seen, and not what they haven’t, thus the statement refers to AOTC Anakin. It’s also in line with Lucas’ vision that ROTJ Vader ~ ROTJ Luke < Jinn.
These quotes could all easily be referencing technical skill. Vader is not the most technically skilled, as you said “he lacks the polish of study with lifelong masters” comparatively Luke’s style is emulated based off of Vader’s but we know that their styles while not as flashy or sophisticated as the PT Jedi allow them to contend.
Vader is the connective tissue to which all things regarding PT vs OT revolve around. If every single PT Jedi were a far greater combatant than Vader why is it that he became known for hunting and murdering them during the purge? How do you reconcile Vader being a terrible duelist that has no relativity to any of the PT Jedi we see, yet he consistently bests them? If you want an example; Roan Shryne and Maki’is are both background characters in Attack of the Clones and Revenge of the Sith respectively, which means that we have “seen them." Vader duels even with Roan Shryne before his faith in the dark side is “firmed” as you quoted. So how come Vader can two-shot Makis in Purge? The only reasonable explanation is that while Vader is not as flamboyant or acrobatic as the Jedi of the prequels and is “an old man” and “half robot” he still possesses the skills and powers to contend and even win a majority of the time. Similarly Ben is not acrobatic or flamboyant, but we know that his skill with a lightsaber was still very deadly.
This reconciled with Lucas’ statement on how we hadn’t seen anything leaves us with a clear conclusion. The moment we truly do see “something” is the Duel of the Fates. When we see a “real JedI” fight a “real Sith”. This is the defining moment in combat, and it’s evident that Jinn > Luke from an intent perspective, as well as from Lucas’ comments.
These quotes also have their own contradictions. For instance Lucas cites Obi-wan being “ready to drop” as the reason that his skill has deteriorated so far, yet ironically enough Dooku is canonically older than Ben, which by Lucas’s and your logic means he would be “frankly shit.”
Why is Kenobi’s lifespan equivalent to Dooku’s? Like, we have people with all kinds of ages in SW, and there’s a clear direct comparison + Lucas quote affirming Kenobi is way worse in the OT.
Section IV - Lightning to Tutaminis
Force lightning is hard to deflect by nature of it’s very properties:
It is with a barrier, yes. But tutaminis creates a 1:1 comparison between the two. Tutaminis is simply energy absorption, and Lightning is obviously energy. The most powerful of masters being challenged by lightning is meaningless, when we see Yoda and Sidious being evenly matched in their lightning to tutaminis clash, and OOU quotes declaring the pair equals.
Yoda having difficulty deflecting it with tutaminis is unsurprising considering that it causes “excruciating pain” and even the “most powerful jedi masters” are “challenged” by deflecting it. This is not a showing of parity whatsoever.
As for your point about Galen’s lightning, that's not how this works. You used Galen’s lightning as your baseline for why Dooku can do the same, I simply asked you to quantify why you think Dooku has as potent of lightning as Starkiller. I don’t have to draw comparisons of power between the two since I wasn’t the one who made the claim. All you did was go in a circle here, provide a connection for why Dooku can do what Starkiller can, the burden of proof is on you.
Simple, Dooku’s ability to press Yoda with it is the evidence I need. I’ve literally cited a dozen instances, from C-Canon to G-Canon why Vader is immensely below Yoda. Dooku’s ability to make Yoda struggle is evident of this.
Your interpretation of the lore simply does not fit as well as mine. I have tried tirelessly to explain that due to the Gillard tiering system the gap between Yoda and Dooku is gargantuan, and due to Yoda’s parity with Sidious a being who is “beyond power” to Dooku’s perception there is no hope of Dooku catching up by Revenge of the Sith, And the fact that Kenobi is relativistic to Dooku means Yoda is vastly beyond him anyway. That leaves us with three options. Either:
-Dooku has all these great showings but with stipulations attached so that Yoda is not as powerful as he would be as a nine.
-Dooku has very specific advantages against Yoda that won’t be there against Vader.
-Or, Yoda experiences some great amount of growth in the period between YDR and Revenge of the Sith that renders the entire comparison moot.
Except the gaps between Gillardian tiers are subjective. As I’ve given an example of before, .1% of an immense quantity is still “enormous”. 0.1% percent of a trillion dollars is still an immense quantity. Yoda possesses immense power, so the idea that Gillardian tiers magically mean that Yoda stomps Dooku in his prime is completely bullshit. Kenobi isn’t near Dooku, so thus your three options are rendered moot.
Did I ever deny Ben’s inferiority to his Mustafar “letting go” form? My argument was built around the premise that the level of deterioration he experienced was canceled out by the growth he shows throughout Revenge of the Sith. Luke does have more raw power then Ben, you would know that if you actually read my quotes. He is also more skilled, something I’ve already substantiated that you seemed to ignore.
Yet Mustafar Kenobi ~ IH Kenobi, as that realization means shit in terms of power.
So, why would Vader not use a barrier if he is aware of his weakness to lightning? Why would he try to counter it with something he knows is ineffective. Against the Starkiller clone he was facing an equal, so it makes sense that the bursts would get through on chance occasions, but even then all it did was slow him down. Prove to me why Dooku is on Starkiller’s level lightning wise and prove to me how this weakness is so absolute that it assures Dooku victory. Then articulate why Dooku’s dueling skills are so exorbitantly above Vader’s that he can mitigate Vader’s colossal strength advantage and superior durability, or why Dooku is able to just ragdoll him outright and why that would stop Vader.
Barriers are good against TK. Not against lightning. Logically, they’re bad against them, because a barrier is a bubble of TK, whereas Tutaminis, an ability Vader has shown little proficiency in compared to Yoda creates a 1:1 comparison between the two. Given that Vader having superior physical strength is debunked already, and Dooku’s raw power is greatly in excess of Vader’s, it’s evident why Dooku wins this.
That’s one way things could happen. Another is what happened during The Force Unleashed (which is far closer to the mature Vader I am debating with) where Vader’s attacks “redouble” and he becomes infinitely more deadly. Wouldn’t it be equally likely things played out as they did on the Invisible Hand but this time Dooku’s taunt backfired causing Vader to get mad and simply overpower him?
But does Starkiller use Padme, Vader’s one emotional weakness against him? Vader goes into a berserk rage when taunted about her, it’s evident that he’d go into one now as well. Dooku’s immense power advantage, tactical advantage, skill advantage, and mobility advantage are all things that will decide this fight in his favor.
Okay, ironically enough you validate my points about Yoda here with Zannah’s quote describing how exhaustive Ataru is. Then you go on to push for this parity to Yoda during the duel which you have yet to describe as anything more than being pushed back for 40 seconds. Again you argue that Anakin is a “Yoda+” to which I raise you the numerous quotes I posted last time claiming Yoda was stronger in the force. To top it off you completely ignored my argument about Dooku getting tired. I don’t care if Anakin had “flashes of brilliance” when we know it was “easy” for Dooku to dismantle both Kenobi and Anakin individually.
This weakness would only get worse by Revenge of the Sith as Dooku notes his body has further physically deteriorated by the time he’s onboard the Invisible Hand:
Dooku doesn’t have the stamina to keep up with Anakin’s blows spending “lavishly his every reserve” just to survive. So, while you can argue all day long about Dooku’s stamina with Yoda, how exhausted he was, Anakin who is not as physically dominating as Vader was already “aging him with every blow.”
Yet the point here being that Dooku’s stamina isn’t bad. Dooku as of ROTS (the iteration I’m arguing, not AOTC) is able to take on Anakin and Obi-Wan for far longer than a minute. Therefore his stamina isn’t dogshit as you’re suggesting, and Dooku’s superior strength in the force mitigates his older body. Funny you bring up Anakin, by the way, because Dooku matches the tier 9 Zonakin in bladelock for 13 seconds with a minor advantage throughout it. Then they disengage and Anakin starts obliterating.
Conclusion
Like ISV, let’s weigh the two shall we?
Dooku has such a greater power advantage that he may be able to ragdoll Vader, but otherwise:
For Team Dooku we have:
- Far greater mobility, skill, and tactics.
- Far greater raw power via a direct comparison (Dooku >> FlashofBrilliance!Anakin >>> AOTC Anakin >>> AOTC Kenobi <= TCW S1 Kenobi > Jinn > ROTJ Luke ~ Vader).
- Comparable, if not superior Strength
- Lightning
For Team Vader we have:
- Superior Durability
It’s clear that Dooku possesses far, far greater advantages than Vader does here, and that Vader doesn’t particularly stand much of a chance.
 IGLevel Four
IGLevel Four
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 4:11 pm
 BreakofDawnLevel Seven
BreakofDawnLevel Seven
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 4:30 pm
Very...interesting conclusions.
 lorenzo.r.2ndLevel Three
lorenzo.r.2ndLevel Three
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 5:53 pm
big agree lolBoD wrote:Very...interesting conclusions.
 Nute_ChethrayModerator
Nute_ChethrayModerator
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 5:59 pm
Great post, though a few points seemed somewhat...farfetched
 The lord of hungerLevel Two
The lord of hungerLevel Two
 Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
Re: SS - Darth Vader (ISV) vs. Darth Tyranus (IG)
March 14th 2020, 9:26 pm
Page 2 of 3 •  1, 2, 3
1, 2, 3 
 1, 2, 3
1, 2, 3 
- Darth Krayt, Darth Plagueis, Darth Tyranus vs DE Luke, Darth Vader, Darth Caedus
- Darth Maul, Darth Vader & Ventress vs Darth Tyranus, Darth Nox & Darth Malgus
- SS - Darth Tyranus (ArkhamAsylum3) vs Darth Vader (DC77)
- SS - Darth Tyranus (BreakofDawn) vs Darth Vader (Shioz)
- SS - Mace Windu (KnightfallVader / alex s) vs Darth Tyranus (Darth Dorin's Baneling)
Permissions in this forum:
You cannot reply to topics in this forum|
|
|



